Viscous Terms

Momentum Equation

The viscous terms from the momentum equation are

(1)\[vis_i = \frac{\partial \sigma_{ij}}{\partial x_j} = \frac{\partial}{\partial x_j}\left[ 2\mu S_{ij} - \left( p + \frac{2}{3}\mu S_{kk} \right)\delta_{ij} \right],\]

where \(\sigma_{ij}\) is the surface stress tensor, \(\mu\) is the dynamic viscosity, \(p\) is the thermodynamic pressure, \(\delta_{ij}\) is the Kronecker delta, and where \(S_{ij}\) is the strain rate tensor, given by

\[S_{ij} = \frac{1}{2}\left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right).\]

The above two equations may be combined to give

(2)\[vis_i = \frac{\partial \sigma_{ij}}{\partial x_j} = \frac{\partial}{\partial x_j}\left[ \mu \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) - \left( p + \frac{2}{3}\mu S_{kk} \right)\delta_{ij} \right].\]

Before proceeding with a discrete approximation to the viscous terms above it is instructive to write them in an alternative form. Starting from Eq. (1), we can write

(3)\[ \begin{align}\begin{aligned}vis_i = \mu\frac{\partial}{\partial x_j} \left( 2S_{ij} \right) + \frac{\partial\mu}{\partial x_j}\left( 2S_{ij}\right) - \frac{\partial }{\partial x_i} \left( p + \frac{2}{3}\mu S_{kk} \right)\\ = \mu\frac{\partial}{\partial x_j} \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) + \frac{\partial\mu}{\partial x_j}\left( 2S_{ij}\right) - \frac{\partial }{\partial x_i} \left( p + \frac{2}{3}\mu\frac{\partial u_k}{\partial x_k} \right)\\ = \mu\left[ \frac{\partial^2u_i}{\partial x_j\partial x_j} + \frac{\partial }{\partial x_i} \left(\frac{\partial u_j}{\partial x_j}\right) \right] + \frac{\partial\mu}{\partial x_j}\left( 2S_{ij}\right) - \frac{\partial }{\partial x_i} \left( p + \frac{2}{3}\mu\frac{\partial u_k}{\partial x_k} \right)\\ = \mu\left[ \frac{\partial^2u_i}{\partial x_j\partial x_j} + \frac{1}{3}\frac{\partial }{\partial x_i} \left(\frac{\partial u_j}{\partial x_j}\right) \right] + \frac{\partial\mu}{\partial x_j}\left( 2S_{ij} - \frac{2}{3}\frac{\partial u_k}{\partial x_k} \right) - \frac{\partial p}{\partial x_i}\end{aligned}\end{align} \]

The first term in the square brackets is the Laplacian of the velocity and represents the dominant diffusive effect of the viscous terms. It is important to represent this term as accurately as possible in the discrete approximation. The second term in the square brackets is the gradient of the velocity divergence. For low to moderate Mach number atmospheric flows, the velocity divergence is expected to be rather small, and thus this term should have a minimal effect. The next full term is proportional to the viscosity gradient, which may or not be significant depending of the situation. In particular, it is probably negligible for the direct numerical simulation of a laminar atmospheric flow. The term may be significant, however, in a high Reynolds number turbulent flow where the viscosity coefficient \(\mu\) represents the sum of the eddy and molecular viscosities. The final term represents the pressure gradient, which is expected to be important in most cases.

Prior to making a discrete approximation to the viscous terms it is useful to introduce some notation that will make the derivation more compact. Assuming a uniform computational mesh with spacing \(\Delta x\), we define the two- and three-point first difference operators as

(4)\[\frac{\delta_1\phi}{\delta_1x} \equiv \frac{ \phi_{i+1} - \phi_i }{ \Delta x } = \left.\frac{\partial\phi}{\partial x}\right\vert_{i+1/2} + O(\Delta x^2)\]

and

(5)\[\frac{\delta_2\phi}{\delta_2x} \equiv \frac{ \phi_{i+1} - \phi_{i-1} }{ 2\Delta x } = \left.\frac{\partial\phi}{\partial x}\right\vert_{i} + O(\Delta x^2)\]

and the three-point second difference operator as

(6)\[\frac{\delta_2^2\phi}{\delta_2x^2} \equiv \frac{ \phi_{i+1} - 2\phi_i + \phi_{i-1} }{ \Delta x^2 } \simeq \left.\frac{\partial^2\phi}{\partial x^2}\right\vert_{i} + + O(\Delta x^2)\]

Note that the symbol \(\delta\) is used somewhat ambiguously to mean either the Kronecker delta (as in Eq (1)), or the finite difference operator (as used above). The number and format of the subscripts are different, however, and this is used to distinguish between the two. It will also be convenient to define the two-point interpolation operator as

(7)\[{\overline{\phi}}^{1x} \equiv \frac{1}{2}\left( \phi_{i+1} + \phi_i \right) = \phi_{i+1/2} + O(\Delta x^2)\]

As indicated, all of the above discrete approximations are second order accurate at the indicated grid location. The need for the midpoint locations \(i+1/2\) will become apparent below (see Figure Fig. 11).

Use the definitions above, it is possible to derive the following identities, which will come in handy in the derivation to be performed below.

\[\begin{split}\begin{eqnarray} \overline{\frac{\delta_1\phi}{\delta_1x}}^{1x} = \frac{\delta_1\overline{\phi}^{1x}}{\delta_1x} & = & \frac{\delta_2\phi}{\delta_2x}\\[0.1in] \frac{\delta_1}{\delta_1x}\left(\frac{\delta_1\phi}{\delta_1x}\right) & = & \frac{\delta_2^2\phi}{\delta_2x^2}\\[0.1in] \frac{\delta_n}{\delta_nx}\left(\frac{\delta_n\phi}{\delta_ny}\right) & = & \frac{\delta_n}{\delta_ny}\left(\frac{\delta_n\phi}{\delta_nx}\right) \end{eqnarray}\end{split}\]

In the finite volume context we work work with an integral form of the conservation laws. If we integrate the momentum equation over a single computational cell and concentrate on the viscous terms, we can write

(8)\[\frac{\partial \rho u_i}{\partial t} \;\sim\; \frac{1}{\mathcal{V}}\int_\mathcal{V} vis_i d\mathcal{V} \;=\; \frac{1}{\mathcal{V}}\int_\mathcal{V} \frac{\partial \sigma_{ij}}{\partial x_j} d\mathcal{V} \;=\; \frac{1}{\mathcal{V}}\int_S \sigma_{ij} n_j d\mathcal{S} \;\simeq\; \frac{1}{\mathcal{V}}\sum_{l=1}^{6~faces} \left[\sigma_{ij} (n_j\Delta \mathcal{S})\right]_l\]

where the sum in the final term is taken over the six faces of the computational cell, having area-weighted, outward-pointing, normal vectors \([(n\Delta \mathcal{S})_j]_l~~\scriptsize{j=1,2,3},~~~~ \scriptsize{l=1,2,...,6}\). Since the solution variables are stored at the cell centers, interpolation must be used to calculate the viscous terms (diffusive fluxes) at the cell faces. The basic idea can be illustrated using an \(x-y\) cross-section of a Cartesian mesh as shown below.

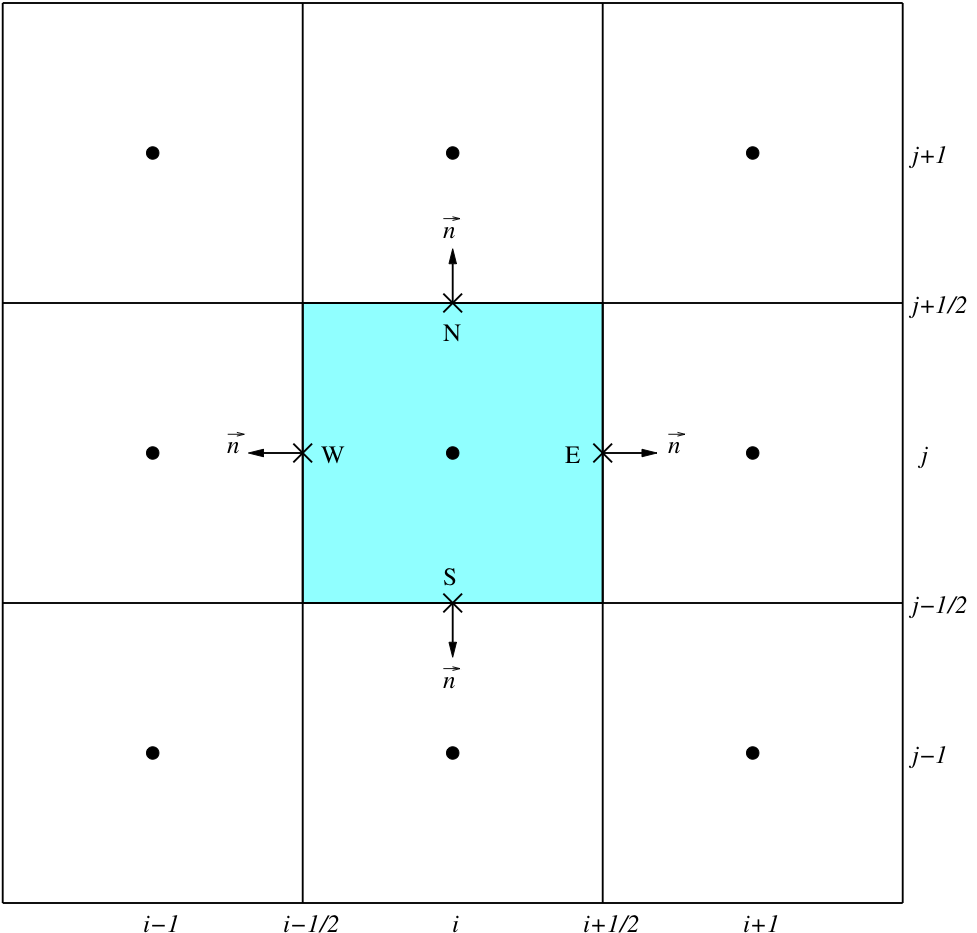
Fig. 11 Finite volume data layout in the x-y plane. The solution variables are stored at the cell centers (filled circles) and the fluxes are computed at the cell faces ('X' symbols).

Here the locations of the solution variables are denoted filled circles whereas the locations of the cell faces where the fluxes must be computed for cell \((i,j)\) are denoted with 'X' symbols. These points are labeled N, S, E, and W in analogy with compass coordinates. The geometric terms \((n\Delta\mathcal{S})_j\) for the faces N, S, E, and W are \((0,1,0)\Delta x\Delta z\), \((0,-1,0)\Delta x\Delta z\), \((1,0,0)\Delta y\Delta z\), and \((-1,0,0)\Delta y\Delta z\), respectively, where \(\Delta z\) the mesh spacing in the direction perpendicular to the plane of the sketch. The area-weighted normal vectors for the faces with normals perpendicular to the plane of the sketch are \((0,0,1)\Delta x\Delta y\), and \((0,0,-1)\Delta x\Delta y\) Using this information, the discrete approximation to the sum of the viscous fluxes is

\begin{eqnarray} \frac{1}{\mathcal{V}}\sum_{l=1}^{6~faces} \left[\sigma_{ij} (n_j\Delta \mathcal{S})\right]_l & = & \left[ \left(\sigma_{i1}\right)_{i+1/2,j,k} - \left(\sigma_{i1}\right)_{i-1/2,j,k} \right] \frac{\Delta y\Delta z}{\Delta x\Delta y\Delta z} \;+ \\ & & \left[ \left(\sigma_{i2}\right)_{i,j+1/2,k} - \left(\sigma_{i2}\right)_{i,j-1/2,k} \right] \frac{\Delta x\Delta z}{\Delta x\Delta y\Delta z} \;+ \\ & & \left[ \left(\sigma_{i3}\right)_{i,j,k+1/2} - \left(\sigma_{i3}\right)_{i,j,k-1/2} \right] \frac{\Delta x\Delta y}{\Delta x\Delta y\Delta z} \\[0.1in] & = & \frac{ \left(\sigma_{i1}\right)_{i+1/2,j,k} - \left(\sigma_{i1}\right)_{i-1/2,j,k} }{\Delta x} \;+ \\ & & \frac{ \left(\sigma_{i2}\right)_{i,j+1/2,k} - \left(\sigma_{i2}\right)_{i,j-1/2,k} }{\Delta y} \;+ \\ & & \frac{ \left(\sigma_{i3}\right)_{i,j,k+1/2} - \left(\sigma_{i3}\right)_{i,j,k-1/2} }{\Delta z} \end{eqnarray}

The fact that the above result is in the form of a finite difference approximation indicates that our finite-volume scheme is equivalent to a correctly-chosen discrete approximation to the differential form of the conservation laws. In particular, it is necessary to evaluate the stress terms midway between the solution points. Notice that the differences above are taken across one grid spacing. Thus using the operator notation above, the discrete approximation can be written as

\[\frac{1}{\mathcal{V}}\sum_{l=1}^{6~faces} \left[\sigma_{ij} (n_j\Delta \mathcal{S})\right]_l = \frac{\delta_1 \sigma_{i1}}{\delta_1x} + \frac{\delta_1 \sigma_{i2}}{\delta_1y} + \frac{\delta_1 \sigma_{i3}}{\delta_1z} \;=\; \frac{\delta_1 \sigma_{ij}}{\delta_1x_j},\]

where it is understood that the stress tensor is to be evaluated at the cell faces. The most straightforward manner to achieve such an evaluation is to compute the derivatives required by \(\sigma_{ij}\) at the cell centers using three-point difference operators, and then interpolate these values to the various cell faces. However doing this would spread the computational stencil across 5 points in each direction, which raises the truncation error and degrades the the spectral characteristics of the diffusion terms at high wavenumber as compared to 3-point operators. Motivated this realization, we form the following discrete approximation to the above equation

(10)\[\frac{1}{\mathcal{V}}\sum_{l=1}^{6~faces} \left[\sigma_{ij} (n_j\Delta \mathcal{S})\right]_l = \frac{\delta_1}{\delta_1x_j}\left[ \underbrace{{\overline{\mu}}^{1x_j} \left( \frac{\delta_1 u_i}{\delta_1x_j} + \frac{{\overline{\delta_2 u_j}}^{1x_j}}{\delta_2 x_i} \right) - \left( {\overline{p}}^{1x_j} + \frac{2}{3}{\overline{\mu}}^{1x_j} \frac{{\overline{\delta_2 u_k}}^{1x_j}}{\delta_2 x_k} \right)\delta_{ij} }_{\normalsize{\tilde{\sigma}_{ij}}} \right],\]

which is different from a straightforward averaging of the stress tensor to the cell face due to the absence of an interpolation operator on the first velocity gradient term, \(\partial_1 u_i/\partial_1 x_j\). Since the data points straddle the face for this term, a two-point difference produces a second order centered approximation at the face (which is at the midpoint of the data). Making this choice keeps the computational stencil more compact, thereby lowering the truncation error and improving the spectral characteristics of the approximation.

Additional insight can be gained by operating on the result above assuming constant viscosity and uniform mesh spacing (both of these constraints can be relaxed at the expense of additional algebraic complexity, but no net change in the conclusions to be drawn below). Under these restrictions, and after a modest amount of simplification, it is possible to rewrite the above relation as

\[\frac{1}{\mathcal{V}}\sum_{l=1}^{6~faces} \left[\sigma_{ij} (n_j\Delta \mathcal{S})\right]_l = \mu\left[ \frac{\delta^2_2 u_i}{\delta_2x_j\delta_2x_j} + \frac{1}{3}\frac{\delta_2}{\delta_2x_i} \left( \frac{\delta_2 u_j}{\delta_2x_j} \right) \right] - \frac{\delta_2 p}{\delta_2x_i}.\]

This is the discrete analog of Eq. (3), written for constant viscosity. Note that our chosen approximation in Eq. (10) results in 3-point operators for the dominant Laplacian and pressure gradient terms. The velocity divergence term can not be written more compactly, but this is not a major concern since we expect it to be negligible.

In order to better understand the advantage of our chosen discritization, consider for a moment the straightforward alternative of uniformly interpolating all elements of the stress tensor to the cell faces. If this is done, the Laplacian term would be approximated as

\[\frac{\partial^2 u_i}{\partial x_j\partial x_j} \simeq \frac{\delta^2_4 u_i}{\delta_4x_j\delta_4x_j},\]

where

(11)\[\frac{\delta^2_4 \phi}{\delta_4x^2} = \frac{\phi_{i+2} - 2\phi_i + \phi_{i-2}}{4\Delta x^2}.\]

This is identical in form to the standard 3-point second difference (Eq. (6)), but effectively using twice the mesh spacing. By skipping over every other point the above formula behaves much like a 3-point operator on a twice coarsened mesh. Since the formula is still second order accurate, the truncation error is increased by a factor of \(2^2=4\). Additional insight can be gained by looking at the spectral characteristics of these two possible second difference operators. To do this note that the Fourier transform of the exact second derivative is

\[\mathcal{F}\left\{\frac{\partial^2\phi(x)}{\partial x^2}\right\} \;=\; -k^2\hat{\phi}(k)\]

where \(k\) is the wavenumber and \(\hat{\phi}(k)\) is the Fourier transform of \(\phi(x)\). The discrete approximations of Eqs. (6) and (11) are

\[\mathcal{F}\left\{\frac{\delta_2^2\phi}{\delta_2x^2}\right\} \;=\; -\underbrace{\frac{2}{\Delta x^2} \left[ 1 - \cos(k\Delta x) \right]}_{{k_m^2}_2} \hat{\phi}(k) \;\simeq\; k^2 - \frac{1}{12}k^4\Delta x^2 + O(k^6\Delta x^4)\]

and

\[\mathcal{F}\left\{\frac{\delta_4^2\phi}{\delta_4x^2}\right\} \;=\; -\underbrace{\frac{1}{2\Delta x^2} \left[ 1 - \cos(2k\Delta x) \right]}_{{k_m^2}_4} \hat{\phi}(k) \;\simeq\; k^2 - \frac{1}{3}k^4\Delta x^2 + O(k^6\Delta x^4)\]

where \({k_m^2}_2\) and \({k_m^2}_4\) are the 'modified wavenumbers (squared)' for the discrete approximations. The Taylor series approximations about \(k=0\) confirms that both approximations are second order accurate and that the truncation error of \(\delta_4^2\phi/\delta_4x\) is four times greater than for \(\delta_2^2\phi/\delta_2x^2\). For turbulence simulation, the behavior of the finite difference approximations at the high frequency end of the spectrum is equally important as turbulent dissipation is focused there. The spectral characteristics of the two alternative approximations are plotted in terms of their associated modified wavenumbers in the figure below.

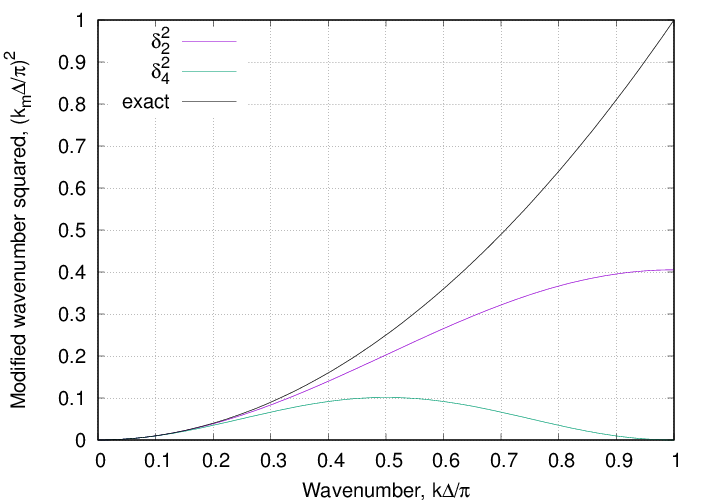
Fig. 12 Modified wavenumbers for three- and five-point second order second differences.

While the three-point approximation is not great for high wavenumbers, the five-point approximation is absolutely terrible. It grossly under predicts the second derivative over all but the first third of the spectral range and actually returns a value of zero for the highest wavenumber! It would be completely unacceptable to use this approximation for turbulence simulations.

Looking beyond accuracy issues, the viscous terms in the momentum equation must obey a few additional physical constraints. Most importantly it is necessary that the viscous terms generate no vorticity for a constant-viscosity fluid. Since the vorticity equation is formed by taking the curl of the momentum equation, it is of interest to take the curl of the viscous terms. This analysis is , the viscous terms (for a constant viscosity fluid) contribute to the time rate of change of \(\omega_z\) via

(12)\[\frac{\partial \omega_z}{\partial t } \sim\]

Energy Equation

The rate of work done by the viscous terms appears in the energy equation as

(13)\[vis\_work = \frac{\partial}{\partial x_j}\left( u_i\sigma_{ij} \right).\]

Using the finite volume approach, simplified for a Cartesian mesh as done for the momentum equation, the work term is approximated as

(14)\[vis\_work \simeq \frac{\delta_1}{\delta_1x_j} \left( \overline{u_i}^{1x_j}\tilde{\sigma}_{ij} \right),\]

where \(\tilde{\sigma}_{ij}\) is defined in Eq. (10).

The energy equation also contains a thermal conduction term that has a form similar to the viscous terms. It is

\[conduction \simeq \frac{\partial}{\partial x_j} \left(k\frac{\partial T}{\partial x_j}\right),\]

which is approximated as

\[conduction \simeq \frac{\delta_1}{\delta_1 x_j} \left(\overline{k}^{1x_j}\frac{\delta_1 T}{\delta_1x_j}\right)\]