This page describes an exact solution to the Taylor-Goldstein equation for
a gravity wave interacting with a thin thermal duct. The duct width h is
assumed to be much less than the GW vertical wavelength. As an example,
we consider a GW with frequency N/3.2 interacting with a duct of width
h=λz/40 and stability increase factor
N2max/N20=4.0.
The exact solution for the vertical velocity is shown below.
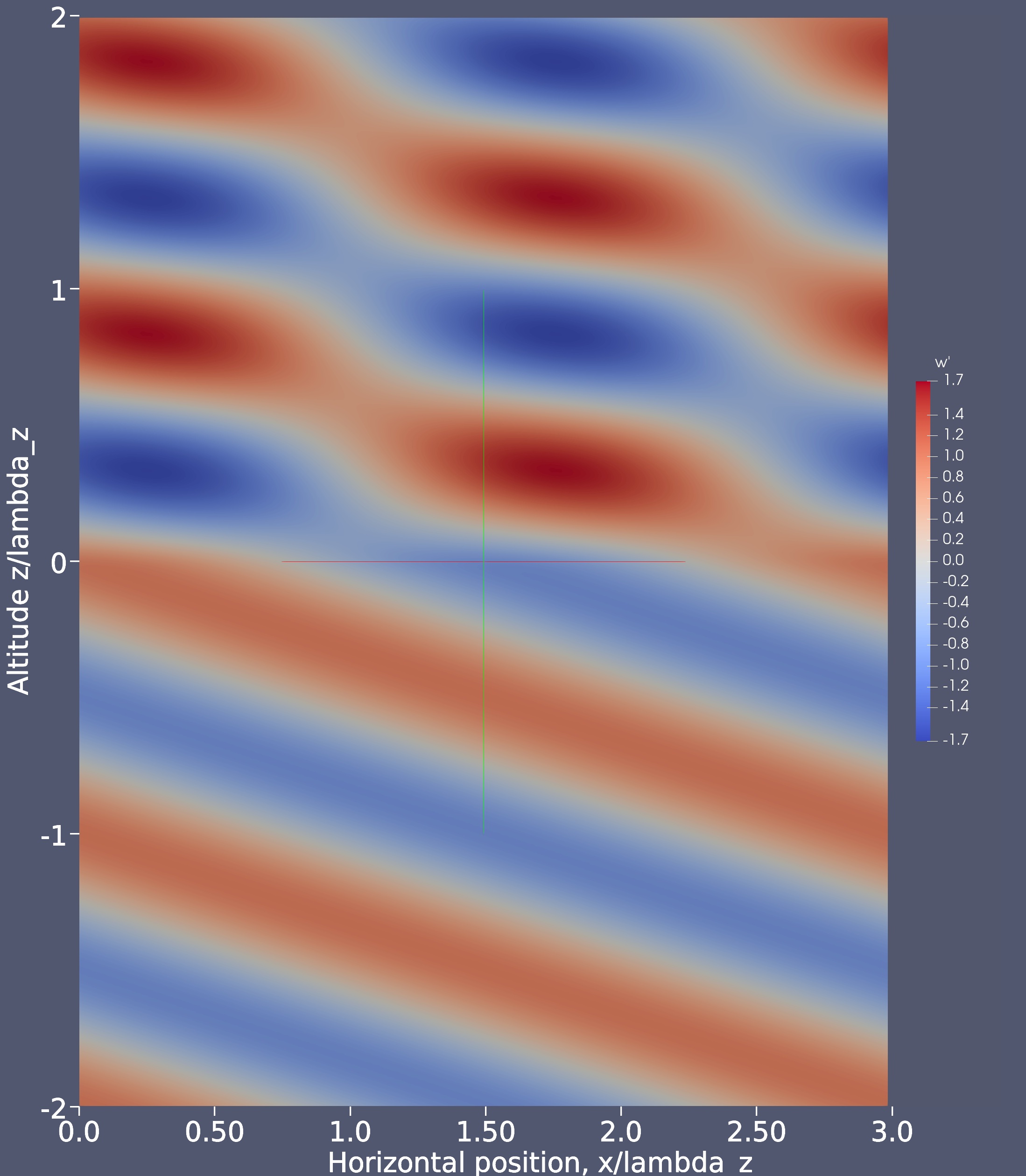
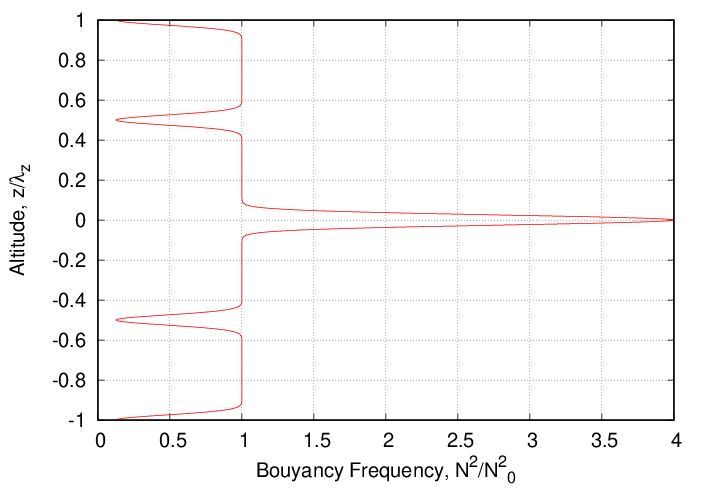
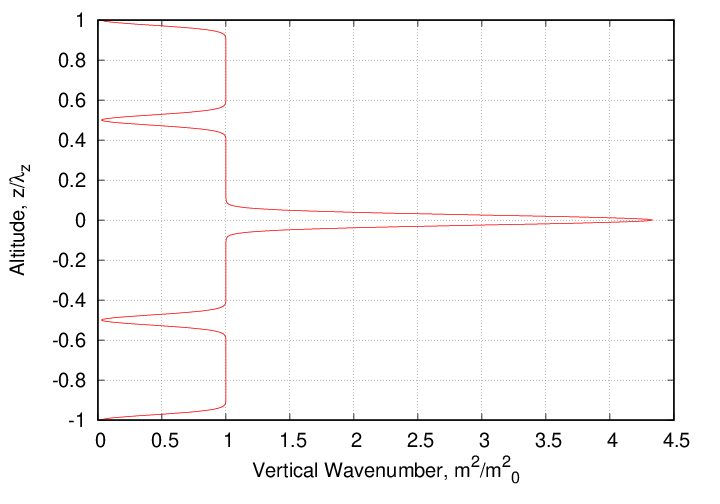
The duct is seen to induce a permanent distortion to the wave field as it passes through. This poses a problem for simulation with a spectral method since the solution is no longer periodic in the vertical direction. Since the duct is so thin, the change to the solution is very abrupt, spanning only the duct width. Since N2 is again constant above the duct, the solution must be composed of simple GW modes. A simple analysis reveals that the distortion imparted by the duct takes the form of the superposition of three modes: the original GW mode and a right- and left-running pair of nearly identical modes but phase-shifted and of reduced amplitude. Since the governing equation is linear of either side of the duct, these additional modes can be canceled by the introduction of an 'anti-duct' above the level of the original duct. If the increase in stability in the primary duct is ΔN2, then simply adding a duct with increment -ΔN2 at distance λz above the original duct will remove the distortions. Unfortunately this solution requires negative N2 and thus is not viable. However, since superposition is valid, we can gradually eliminate the distortions via a collection of weaker anti-ducts. The figures below shows a workable solution where three anti-ducts are used to exactly cancel the distortions.
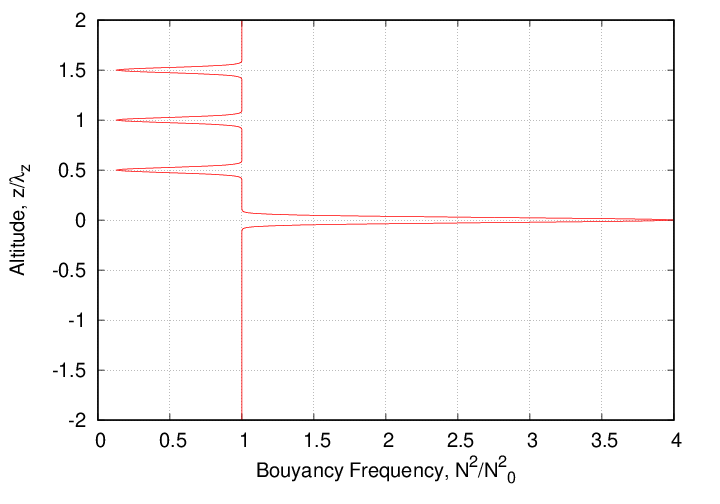
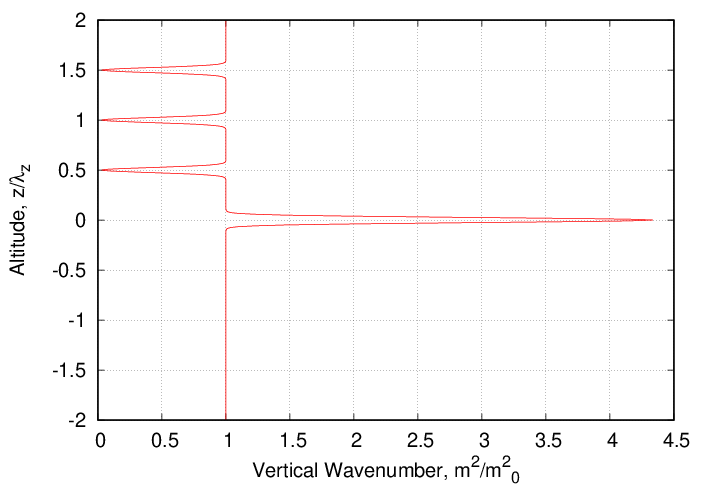
Since the additional modes introduced by the primary duct have been canceled, the solution is again periodic in the vertical direction. The solution is shown here on a larger domain than necessary in order to depict the wave canceling features more clearly. The same solution is shown on a more compact domain below.
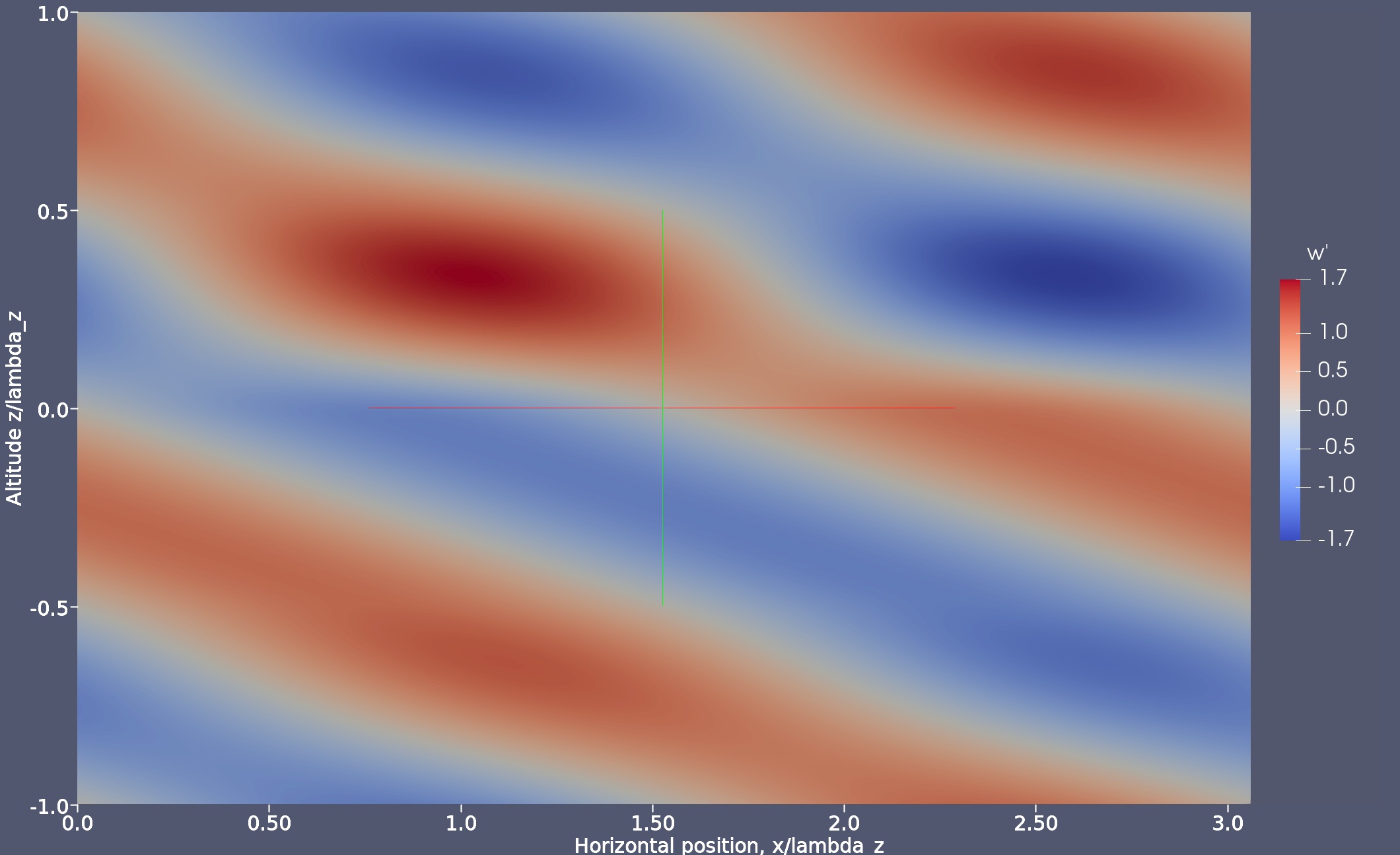
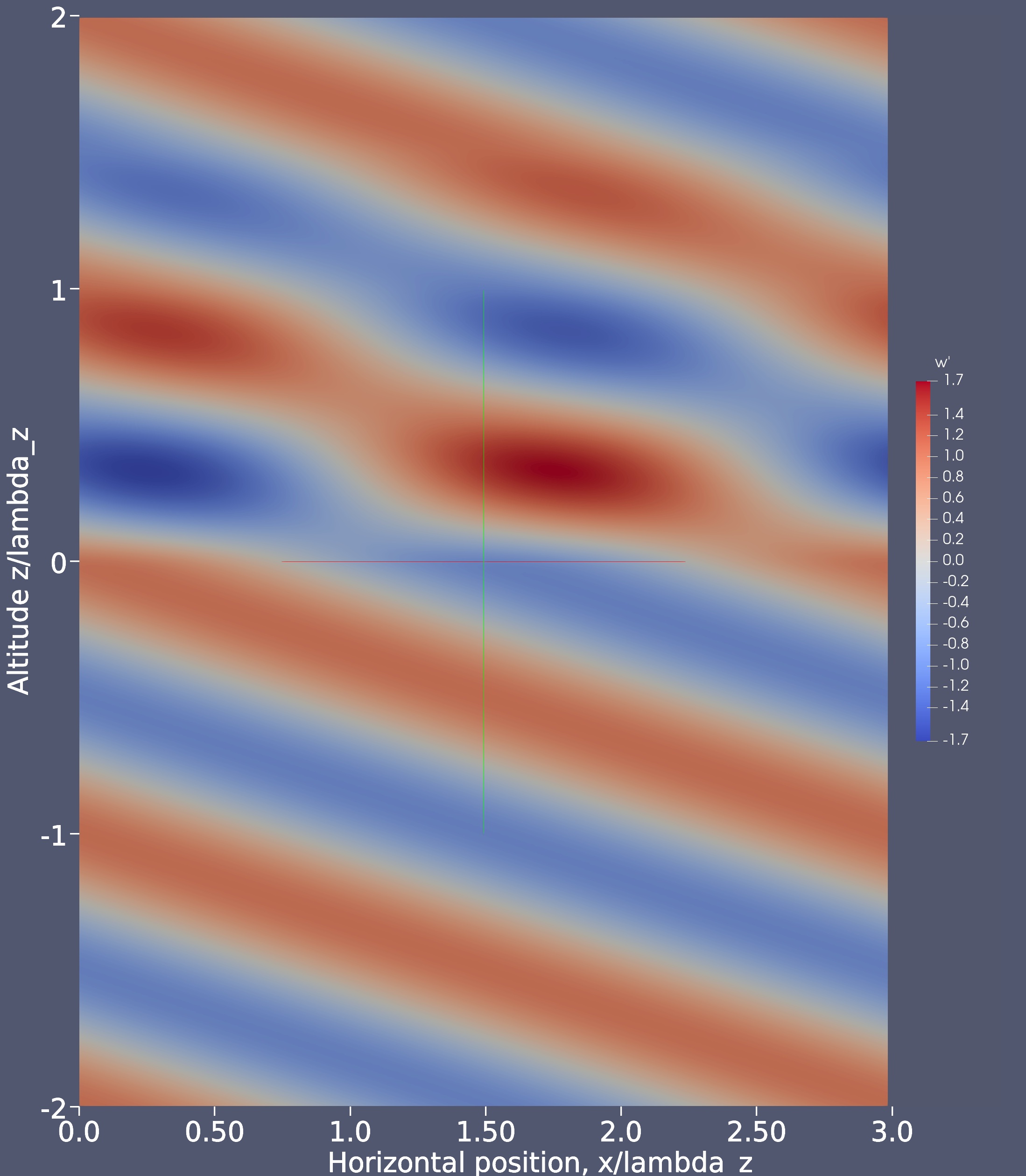
This solution is a bit harder to interpret since the the undisturbed wave exists in the interval between z/λz=[-0.5:0.0].

The duct is seen to induce a permanent distortion to the wave field as it passes through. This poses a problem for simulation with a spectral method since the solution is no longer periodic in the vertical direction. Since the duct is so thin, the change to the solution is very abrupt, spanning only the duct width. Since N2 is again constant above the duct, the solution must be composed of simple GW modes. A simple analysis reveals that the distortion imparted by the duct takes the form of the superposition of three modes: the original GW mode and a right- and left-running pair of nearly identical modes but phase-shifted and of reduced amplitude. Since the governing equation is linear of either side of the duct, these additional modes can be canceled by the introduction of an 'anti-duct' above the level of the original duct. If the increase in stability in the primary duct is ΔN2, then simply adding a duct with increment -ΔN2 at distance λz above the original duct will remove the distortions. Unfortunately this solution requires negative N2 and thus is not viable. However, since superposition is valid, we can gradually eliminate the distortions via a collection of weaker anti-ducts. The figures below shows a workable solution where three anti-ducts are used to exactly cancel the distortions.



Since the additional modes introduced by the primary duct have been canceled, the solution is again periodic in the vertical direction. The solution is shown here on a larger domain than necessary in order to depict the wave canceling features more clearly. The same solution is shown on a more compact domain below.



This solution is a bit harder to interpret since the the undisturbed wave exists in the interval between z/λz=[-0.5:0.0].