Here a series of runs are compared where the details of the filtering strategy
are changed. All runs were performed with the Aug 2 2024 (99698724377) master
branch code, but the behavior of the filter was changed using simple hacks.
The test case is the New Zealand Deepwave case using 4 km horizontal spacing
and 1 km vertical. The entire duration of the forcing is 2 hours and the
simulation time is shifted by 8 hours in order to match with UTC time from the
observations.
The movie below shows a comparison of the vertical velocity for three cases:
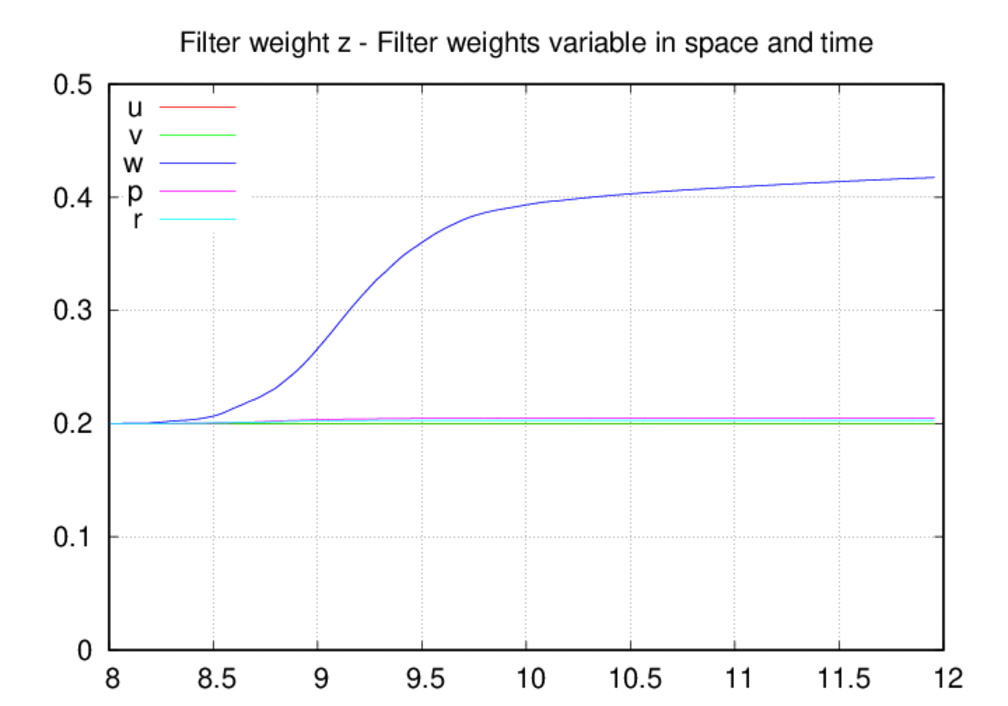
(1) The stock code where the filter weights are variable in both space
and time. The stock values of the filter weight adjustment in time are also
used and these more or less prevent the weights from decreasing in time. (2) A
hacked version where the filter weights do not very in space, but do vary in
time. The filter weight adjustment parameters were also changed so that the
weights can decrease in time. (3) A hacked version where the filter weights
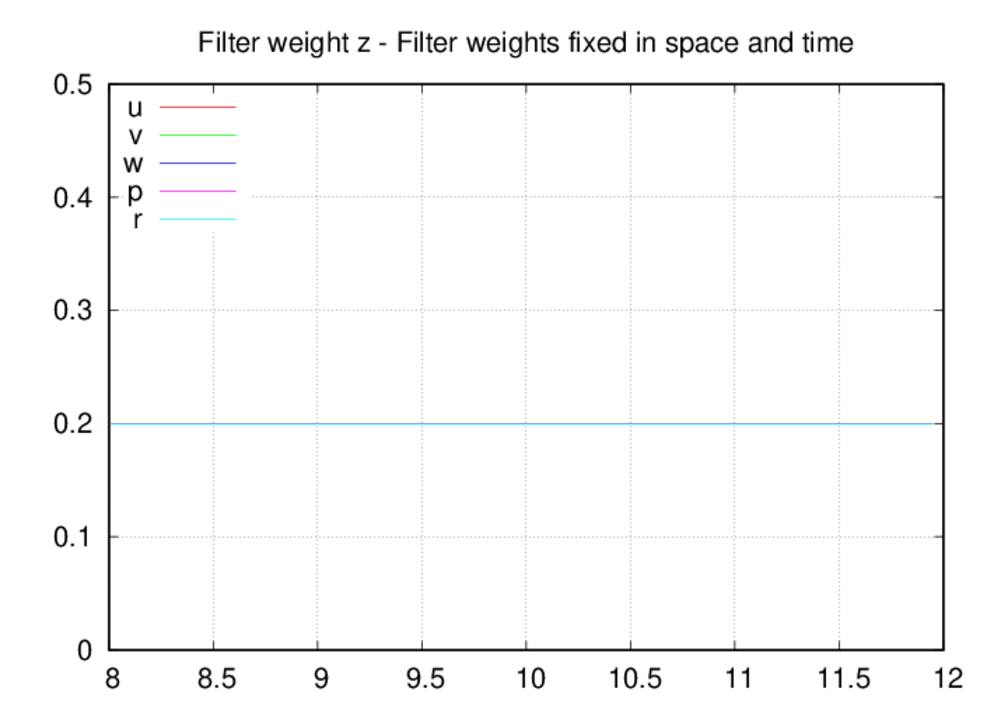
are constrained to be fixed in both space and time. This case should mimic
the old filtering strategy. The constant filter weight was set at 0.20, which
is close to the stability bound (the code will run with a weight of 0.175, but
visible oscillations are present in the solution).
In the following discussion, the case with fully variable weights will be
referred to as the fully-variable case, the case with variable weights
in time only as the fixed-in-space case, and the case with weights fixed in
space and time as the fully-fixed case.
The solutions are nearly indistinguishable from the start to about 8.2 UTC,
when a few oscillations develop in the fixed-in-space case. The oscillations
only persist for a few minutes, however, and then the solutions go back to
being nearly identical until about 9.0 UTC. At this time, acoustic waves
appear near the top of the domain in fully-variable case. Also the
fully-fixed case starts to look over-filtered around this time. Around 9.7
UTC, acoustic noise also appears in the fixed-in-space case. The wave
pattern in the lower portion of the domain for this case is visibly stronger,
and looks more realistic, as compared to the other two cases at this time as
well. The acoustic noise in the fixed-in-time case increases somewhat as we
approach 10.0 UTC, but remains smaller than the fully-variable case. An odd
planar acoustic wave appears in the fixed-in-time case just prior to 10.0
UTC. This defect is unexpected since the forcing scheme is still active and
thus the waves must be generated by a mechanism other than the forcing
endpoint in time. Around 10.10 UTC an acoustic blast is observed in the
fully-variable case, whereas there does not appear to be any additional noise
in the fixed-in-space case. By about 10.30 UTC most of the blast junk has
dissipated and the solutions go back to a situation where the fixed-in-space
case has the strongest, most realistic-looking wave pattern at lower
altitudes, the fully-fixed case looks over-filtered, and both the
fully-variable and fixed-in-space cases show acoustic noise near the top of
the domain. Then from about 10.5 to 11.2 UTC the acoustic noise in the
fixed-in-space case increases and exceeds that present in the fully-variable
case. From about 11.2 UTC to the end of the simulation the noise level in
the upper portion of the domain is reasonably similar between the
fully-variable and fixed-in-space cases.
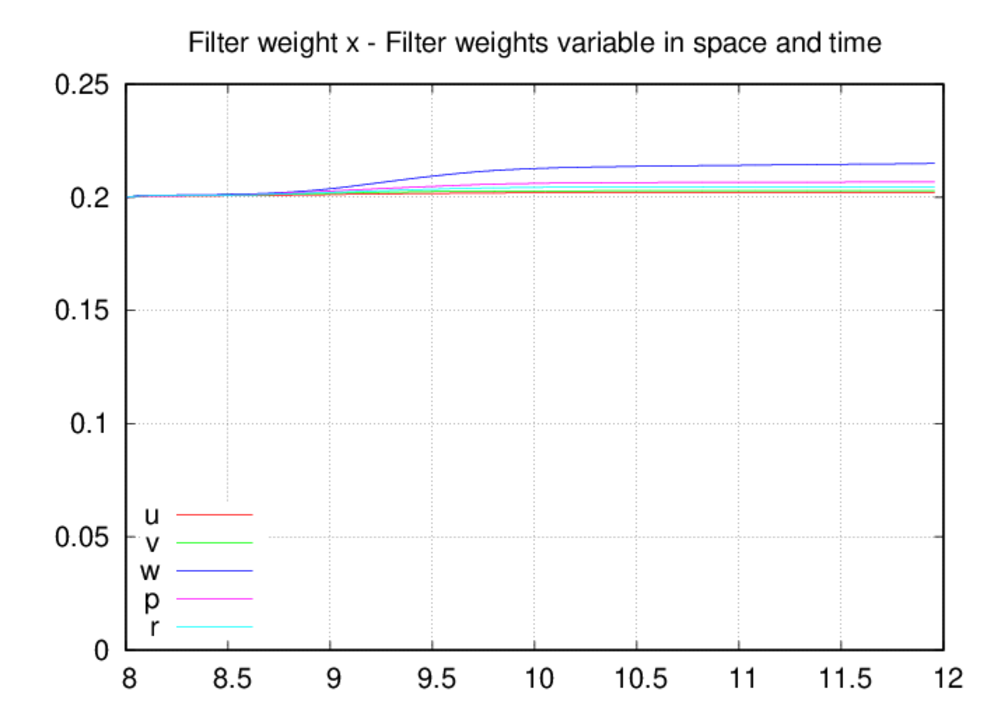
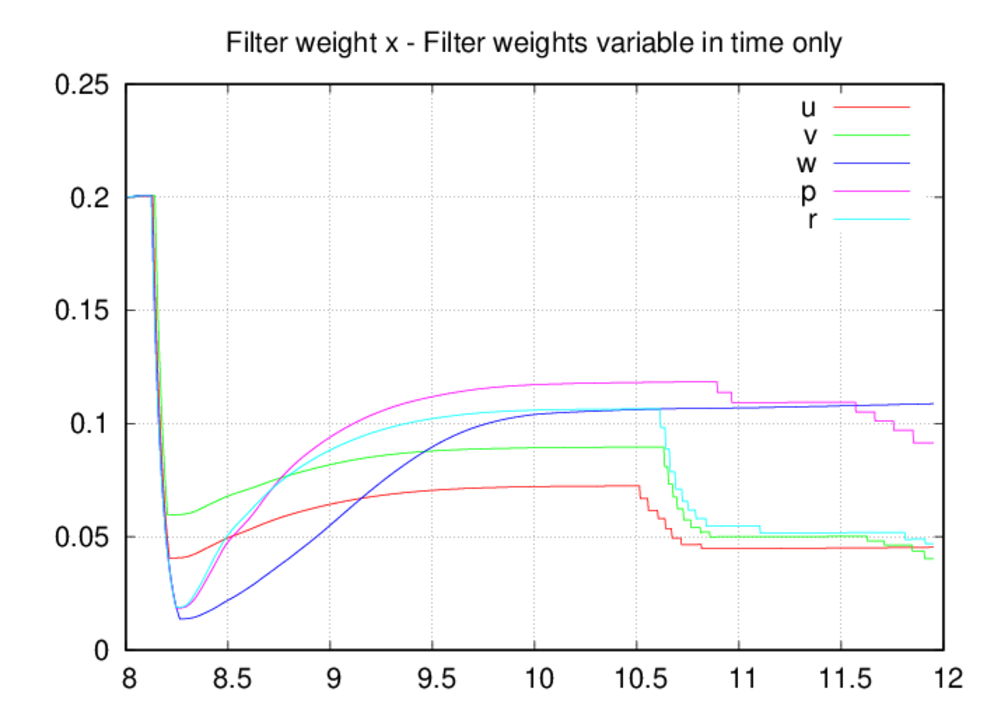
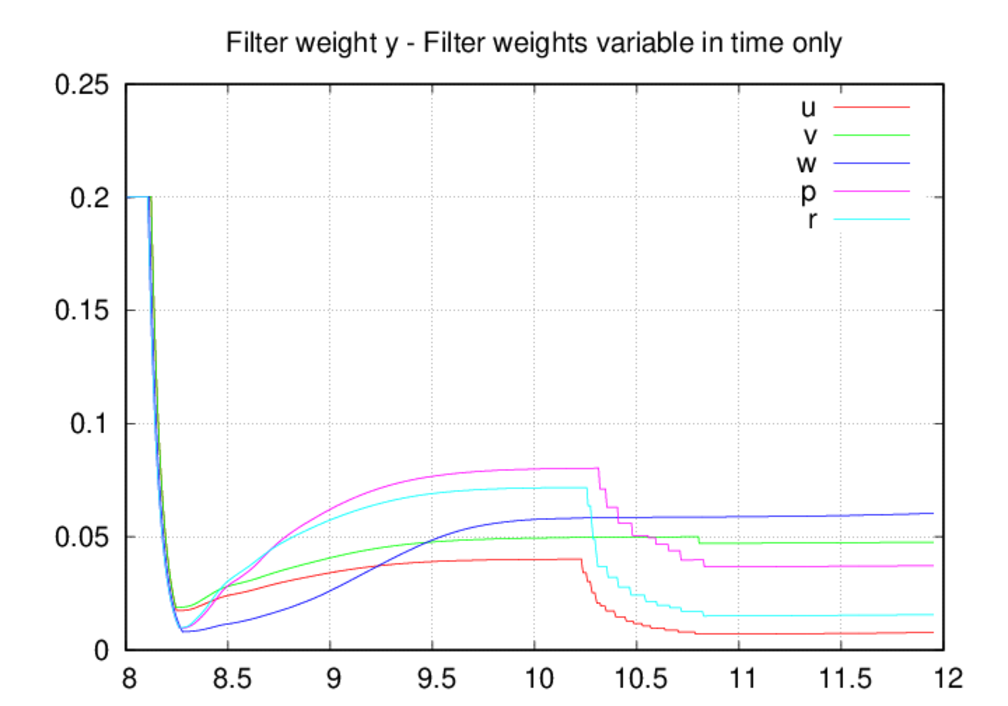
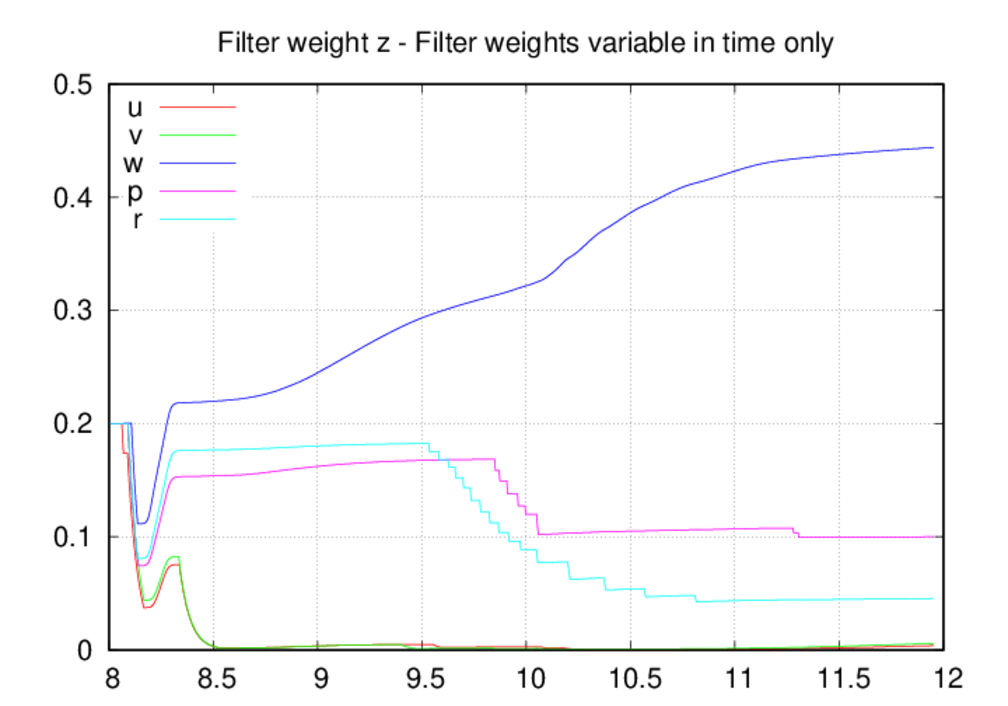
Some of the behavior noted above can be correlated with the filter statistics
shown below. Starting with the filter weight time histories, we see that the
weights in the fully-variable case are effectively constrained to only
increase in time, whereas the weights in the fixed-in-space case can both
increase and decrease. It is also apparent that the rate of decrease
is greater than the rate of increase for the fixed-in-space case (but this
could be corrected with the filt_dec input). When the weights can decrease in
time, we see a fairly strong trend towards smaller filter weights. In fact,
the only weight that exceeds 0.18 is for w in z, and most of the weights are
near or below 0.10. This finding suggests that even the fully-variable case
is probably over-filtered, and the results do show smaller solution
amplitudes compared to the fixed-in-space case.
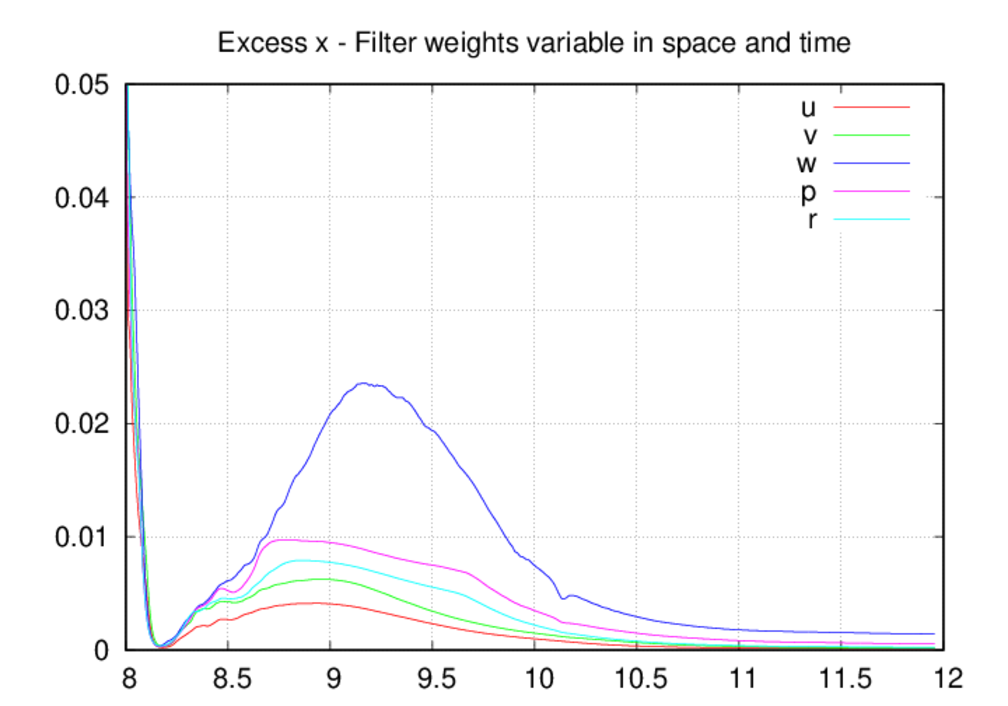
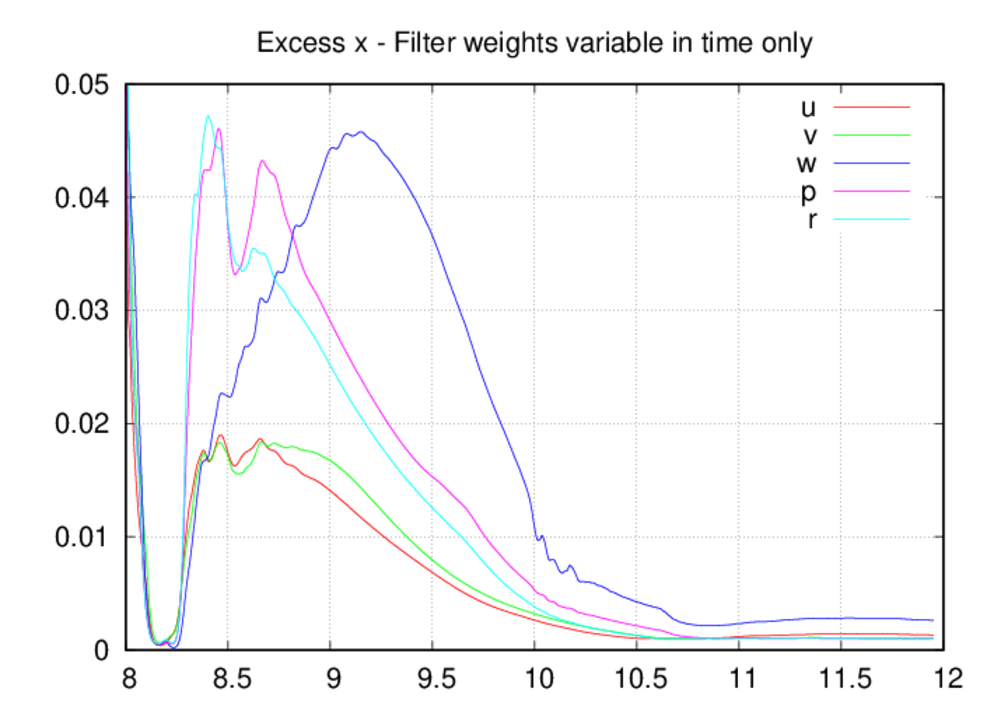
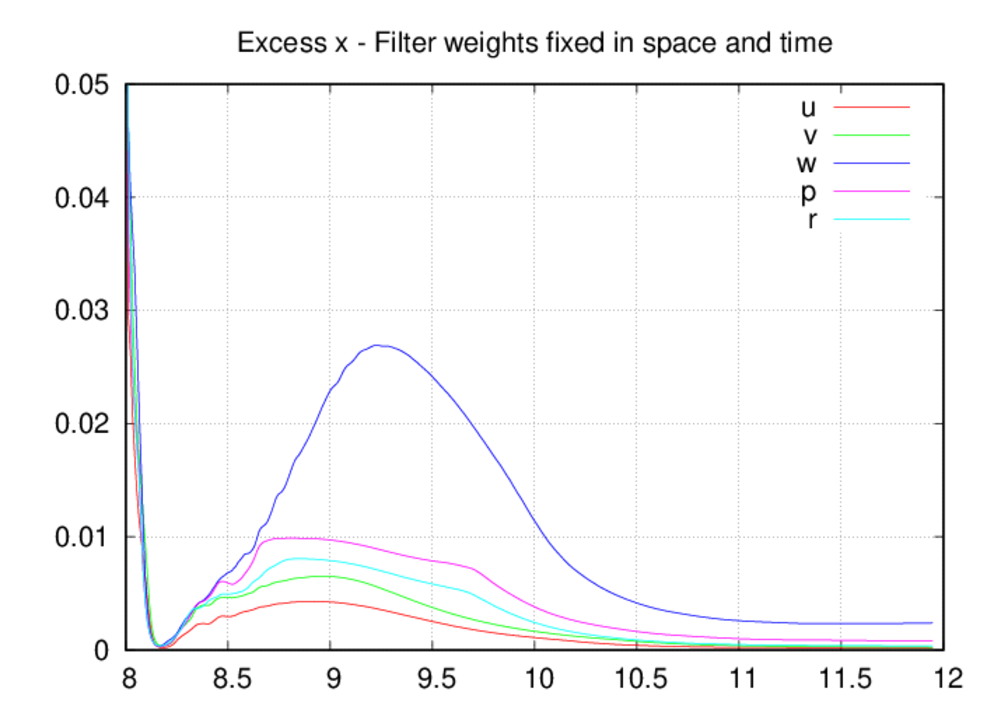
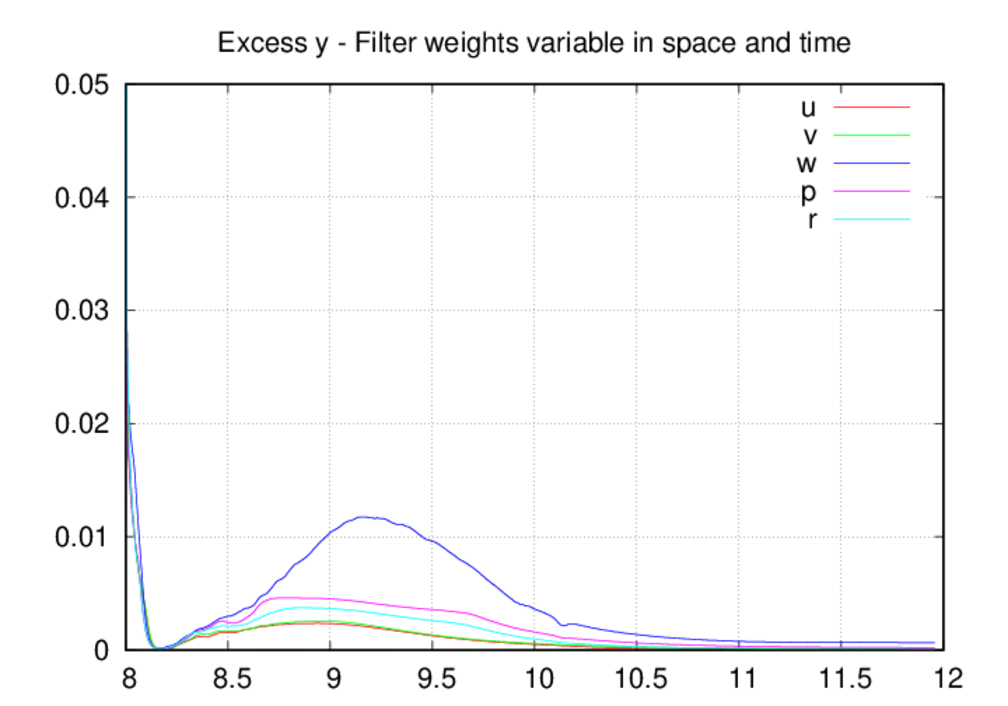
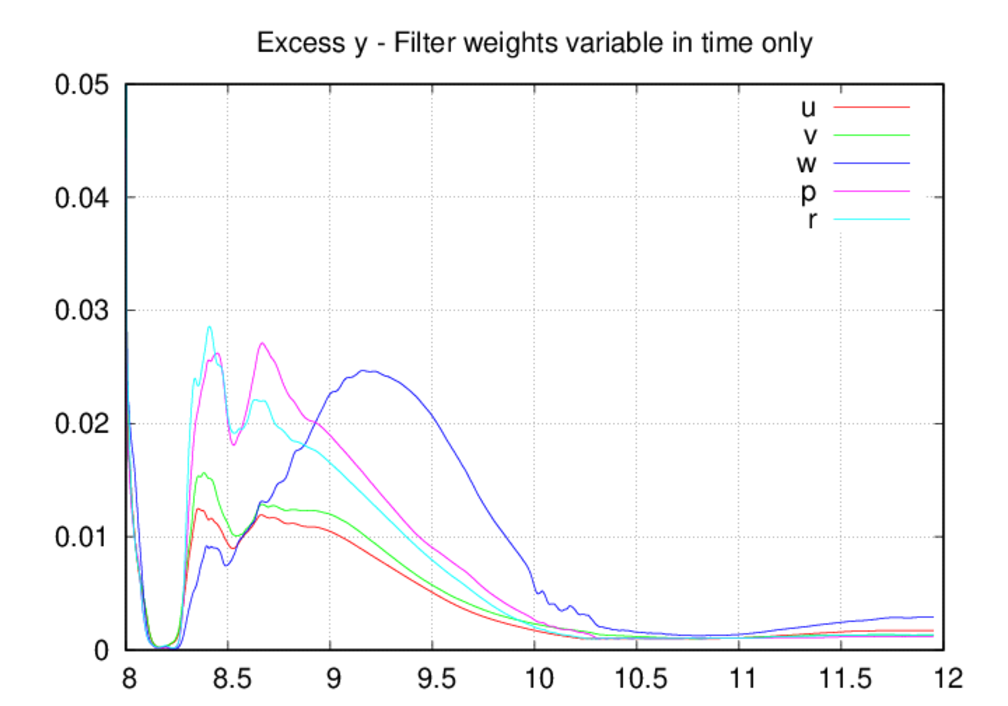
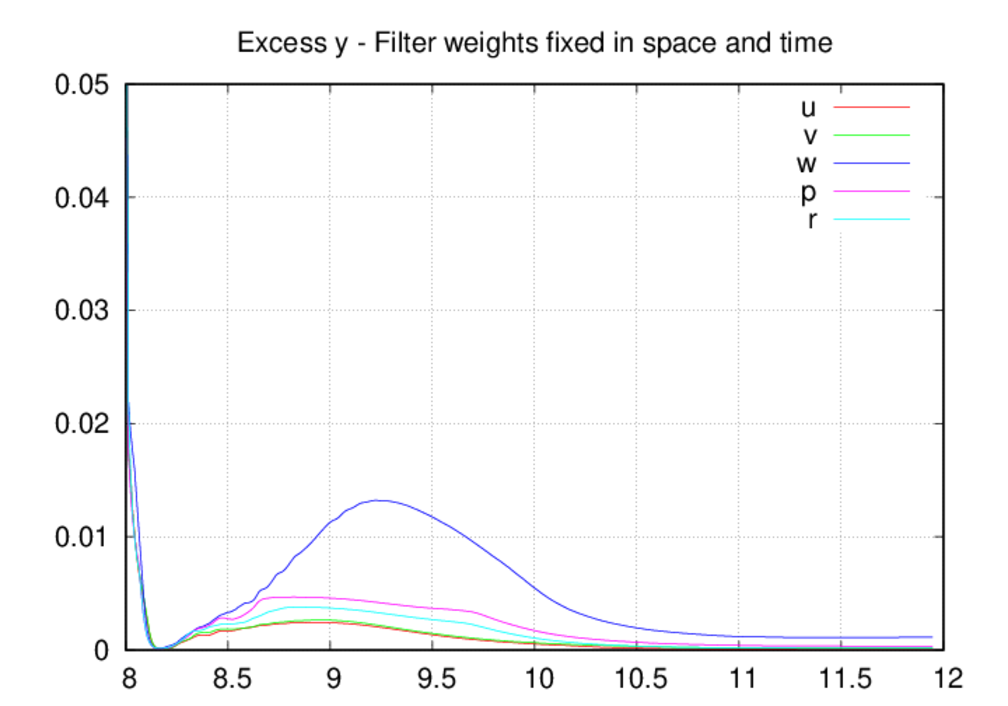
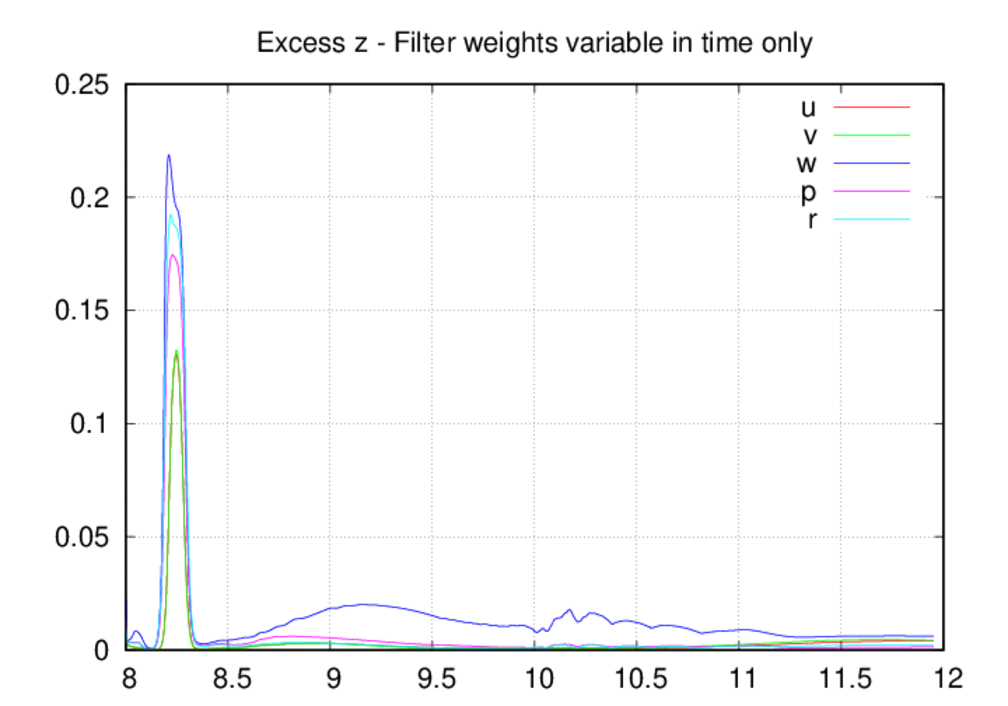
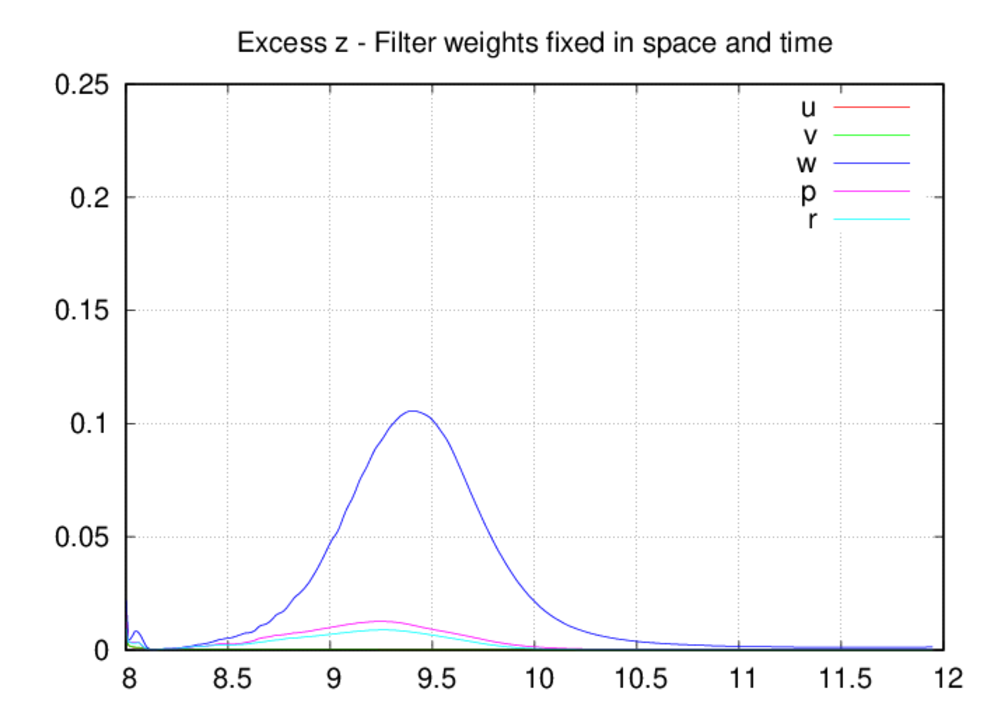
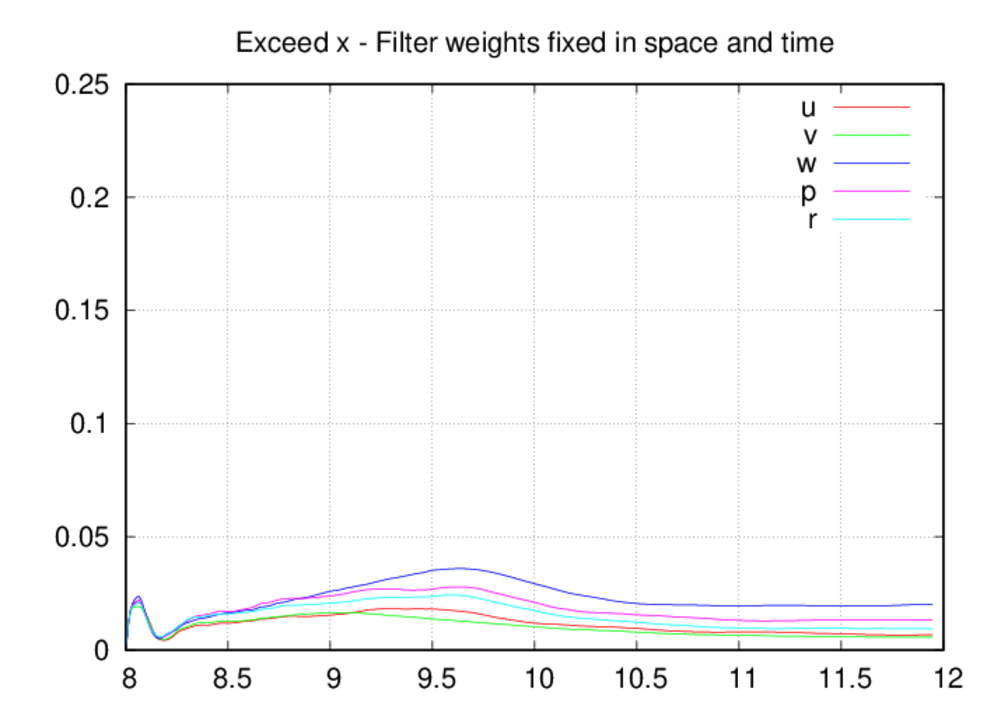
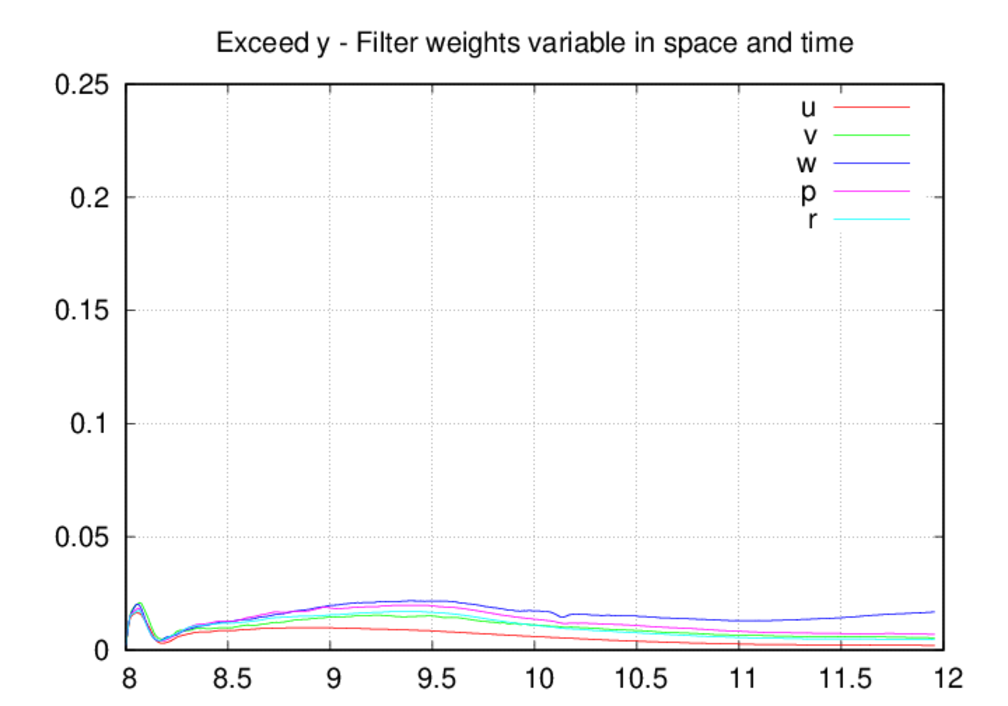
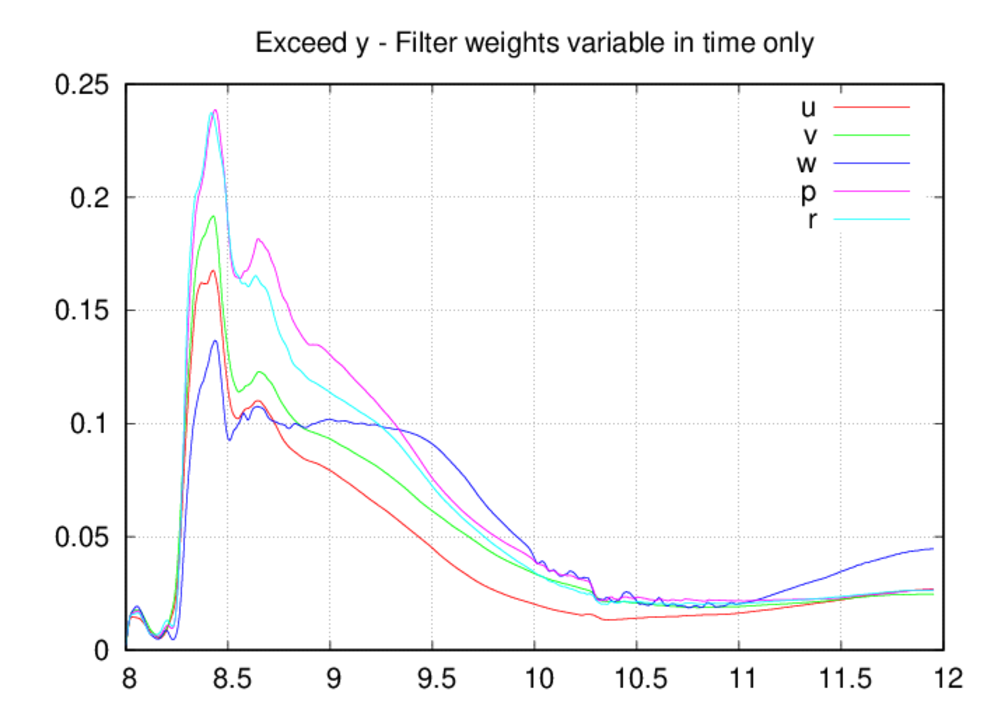
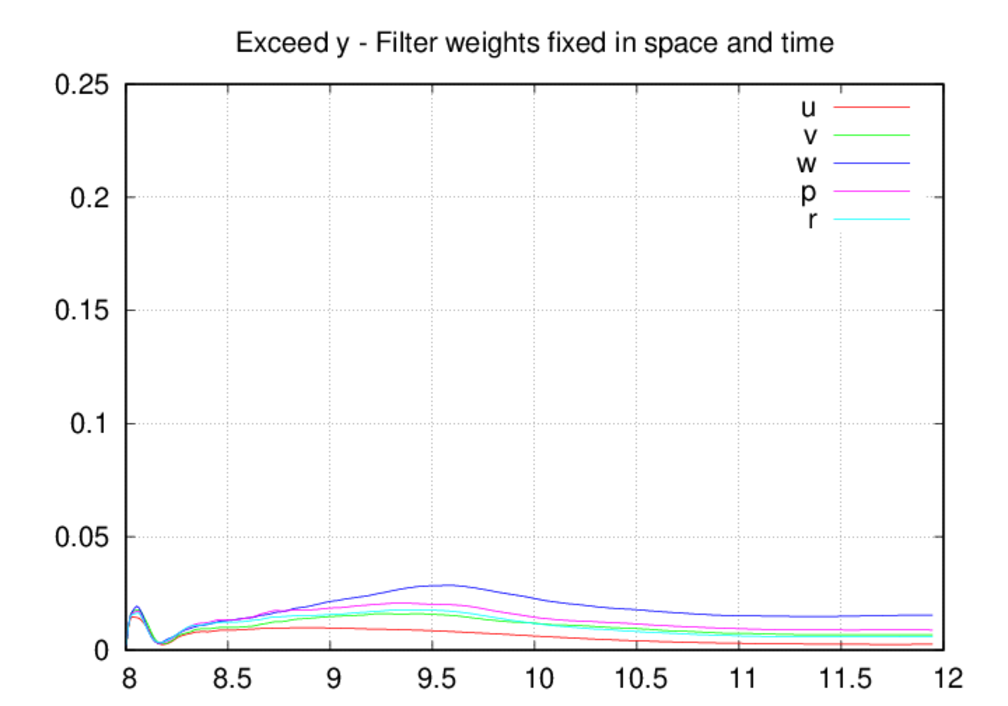
Moving on the the average oscillation excess plots, we see that the oscillation
levels are universally higher in the fixed-in-space case as compared to the
other two. The most likely explanation for this is that, by allowing decreases
in the filter weights, the oscillation levels come into a reasonable
equilibrium as intended by the filter weight control scheme. If the weights
can only increase in time, then they most likely over-filter the solution
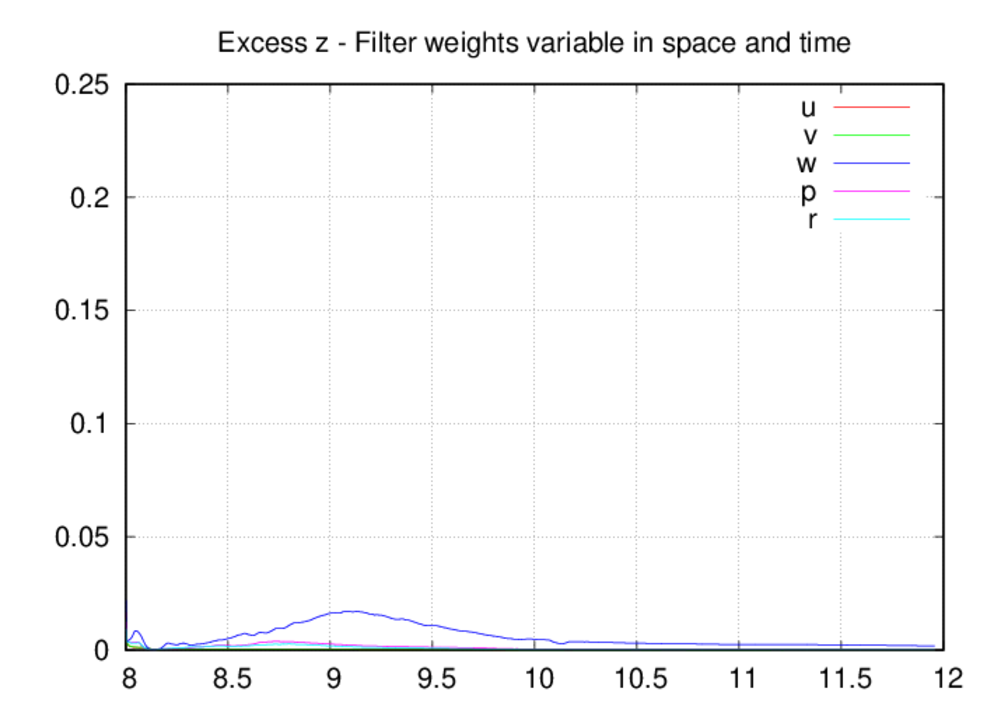
most of the time. The spike in the oscillation excesses in the z direction
around 8.2 UTC is due to the starting acoustic transient as it passes through
the upper portion of the domain, and we saw a clear depiction of these
oscillations in the movie above. Since the filter weights were dropping in
time prior to 8.2 UTC, the scheme is caught off guard as the acoustic blast
enters the upper portion of the domain. The filter weights increase in
response to the threat and the oscillations are controlled.
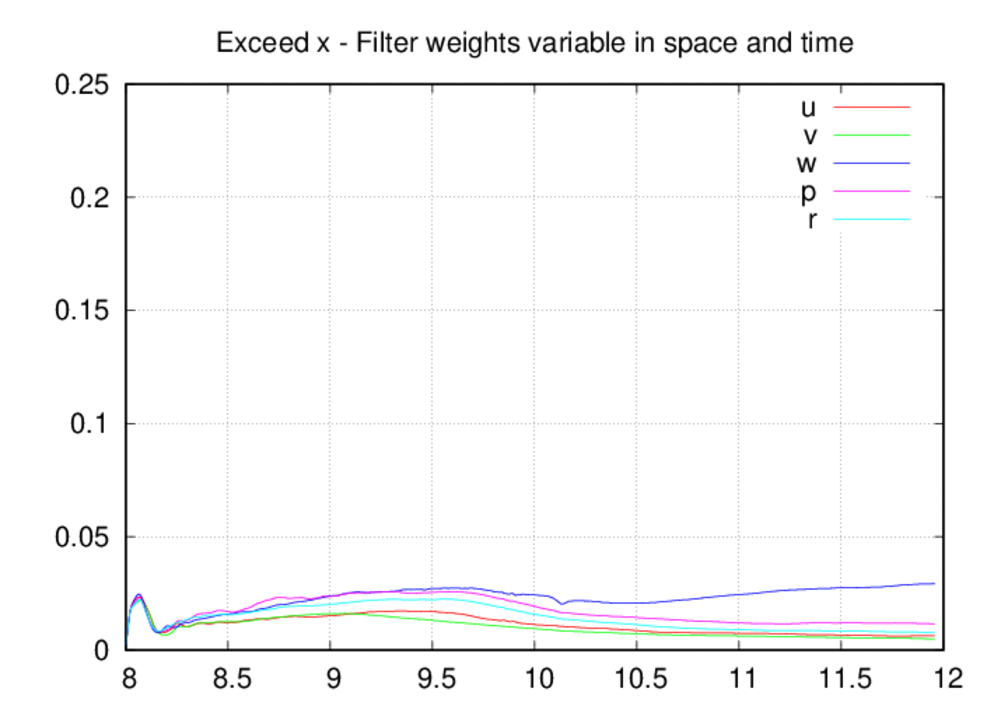
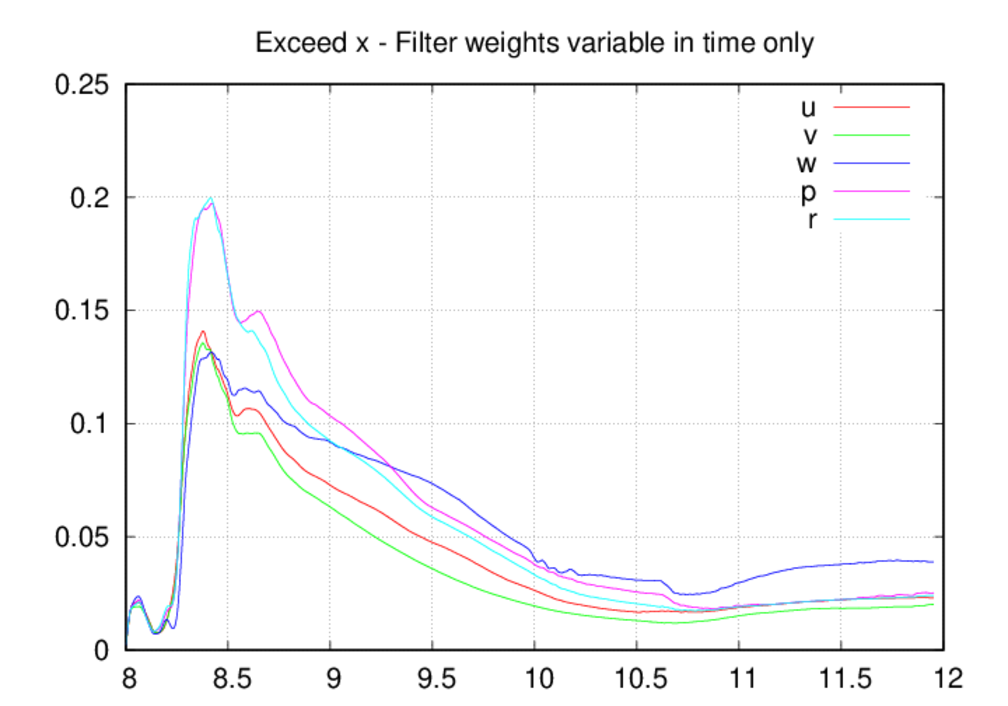
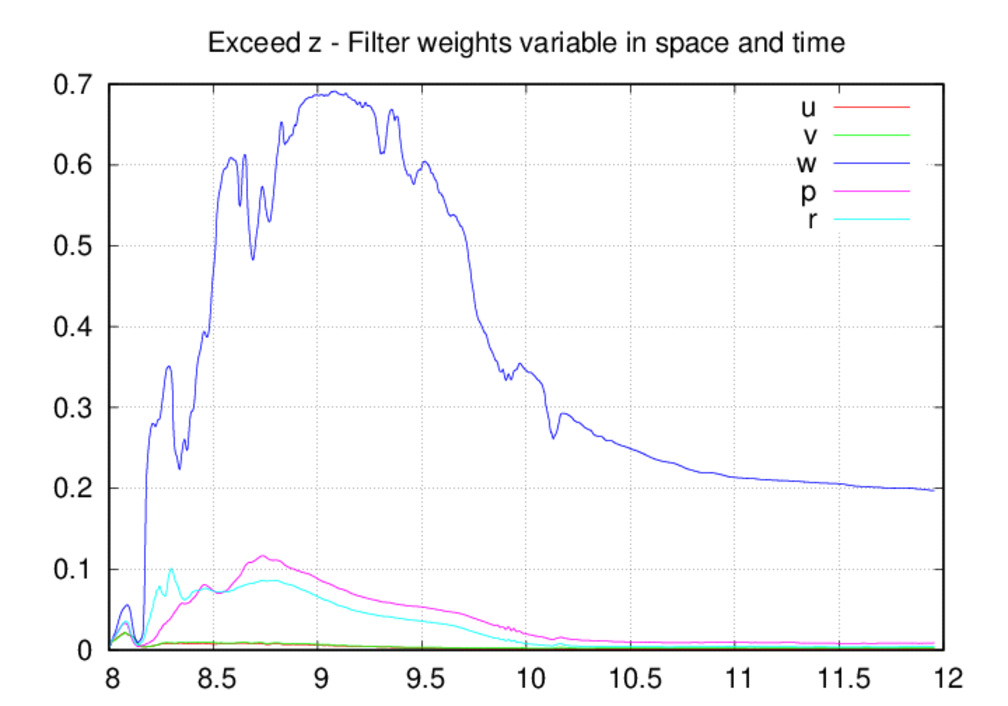
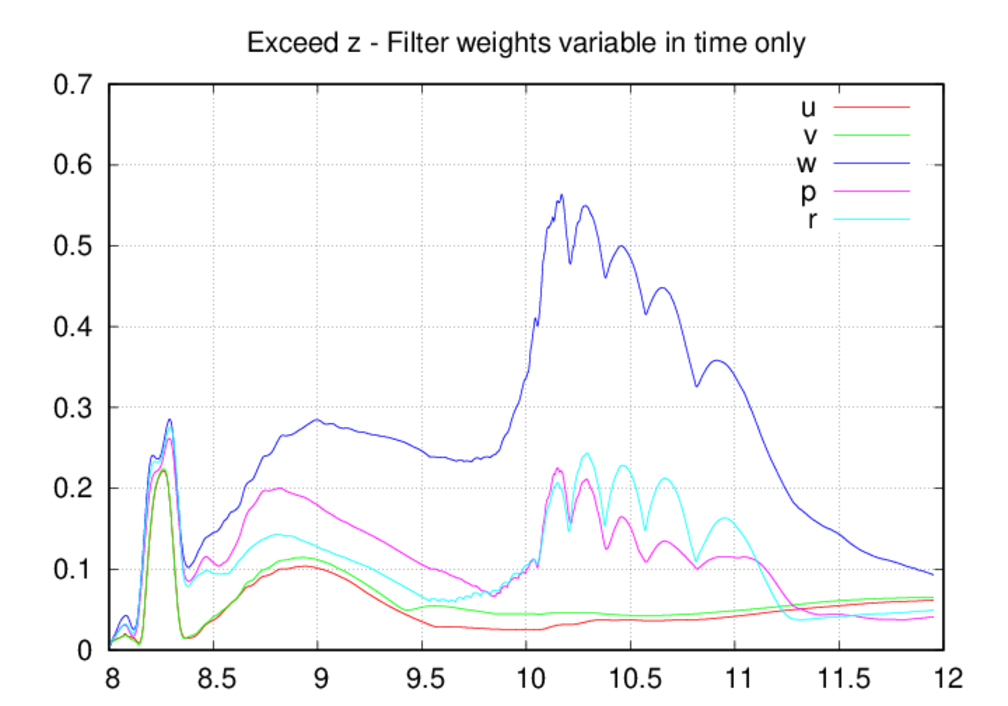
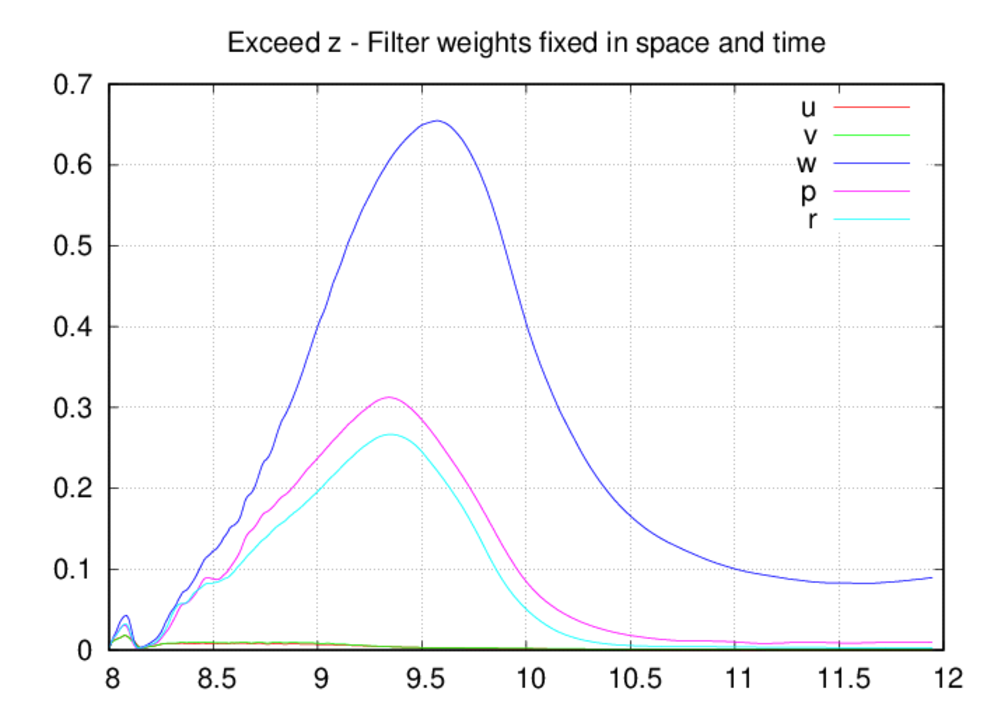
The behavior of the percentage of points over the oscillation target is
similar to the oscillation excess, at least for the x and y directions. In
these directions, the percentages are similar for the fully-variable and
fully-fixed cases, but significantly greater for the fixed-in-space case.
Again the likely reason for this is the ability for the filter weights to
decrease in the fixed-in-space case. The behavior for the oscillation
percentages in the z direction are somewhat more similar for the three cases.
In all of these, the oscillations in w are highly widespread (60-70% of the
points) for at least a half hour period during the simulation. The
oscillations peak close to 9.5 UTC for the fully-variable and fully-fixed
cases, but occur after 10.0 UTC for the fixed-in-space case. The rapid rise
in the oscillation level for this case starting prior to 10.0 UTC correlates
with the planar waves seen in the movie above. There is also a suspicious
periodic behavior in the percentage plots for this case from about 10.0-11.25
UTC, and this also correlates with the time period when acoustic noise is
seen in the upper portion of the domain.