This page describes a series of 2D numerical simulation of mountain wave
generation, focusing on the effects of streamwise grid resolution. The
terrain is a Gaussian approximation to the south peak of the larger Andes
runs, and the wind and temperature profiles from that case are also used.
The vertical mesh is uniformly spaced at 500 m as in the detailed Andes
resolution studies. Since the focus here is on the wave generation and
propagation mechanisms, the top boundary is set at 144 km instead of 200 km,
as was done in the other Andes simulations. Zonal mesh spacings of
1, 2, 4, and 8 km were considered, all having the 500 m uniform mesh
in the vertical. The 1 and 2 km cases were only run out to about
8.0 hours, which is the point where vigorous turbulence overwhelms the
flow solver under the 2D representation. Strong turbulence does not
develop in the 4 and 8 km cases, and these were continued out to a time
of 12 hr.
As discussed below, the results show that the wave strength evolves with an increasing time delay as the mesh is coarsened, and the energy peak moves to larger horizontal scale. The time delay results in smaller wave amplitudes at a given time as the mesh is coarsened. These effects become more pronounced as the mesh becomes very coarse, showing a large drop in wave amplitude (for a fixed time) when moving from 2 to 4 km spacing. Some evidence is provided to suggest that the precipitous drop in wave amplitude for the 4 and 8 km cases is caused by the rapid increase in phase error as the wave is resolved by a small number of grid points per wave length.
Shown below are the zonal velocity perturbations at 7.5 hr for the 4 different mesh resolutions.
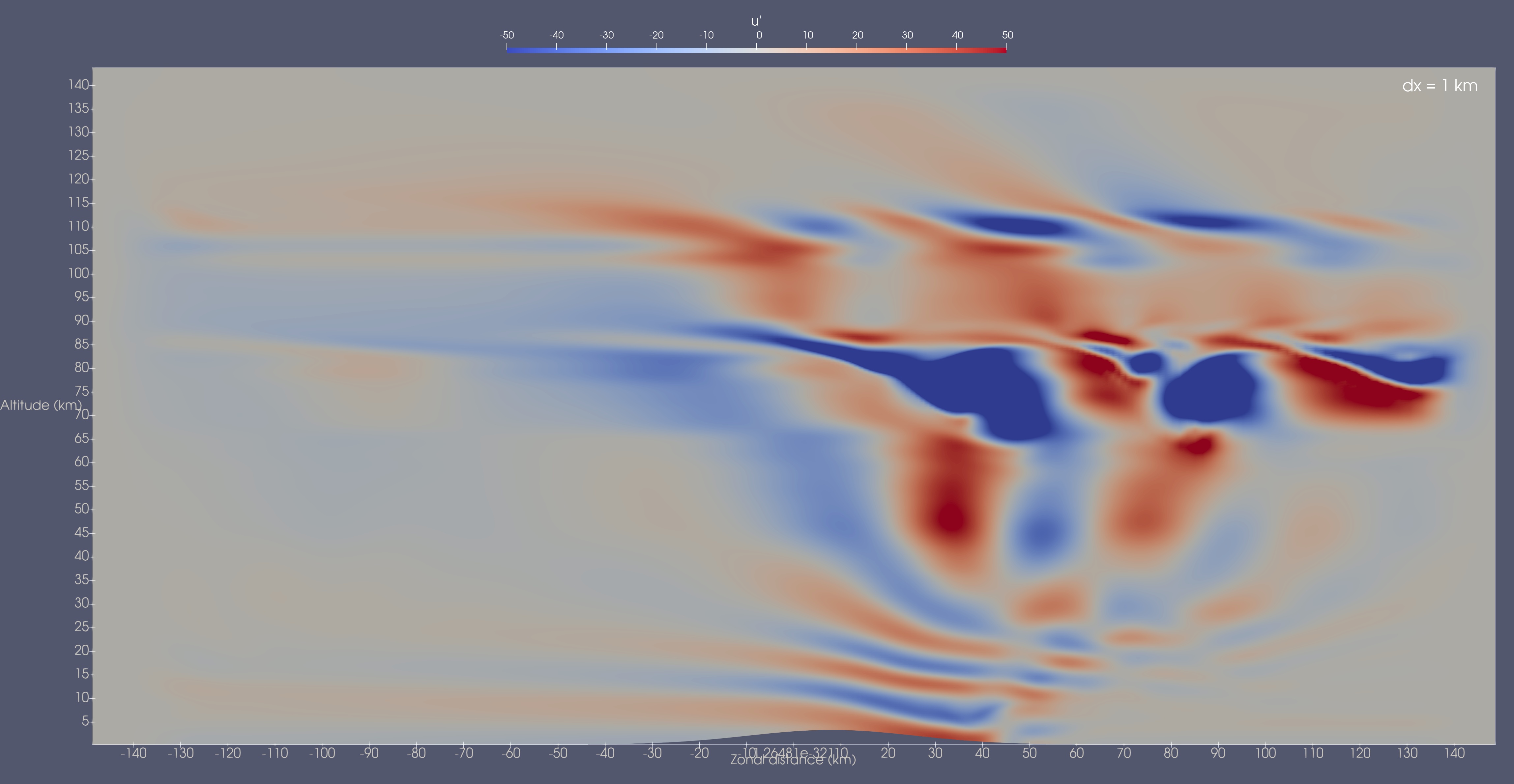
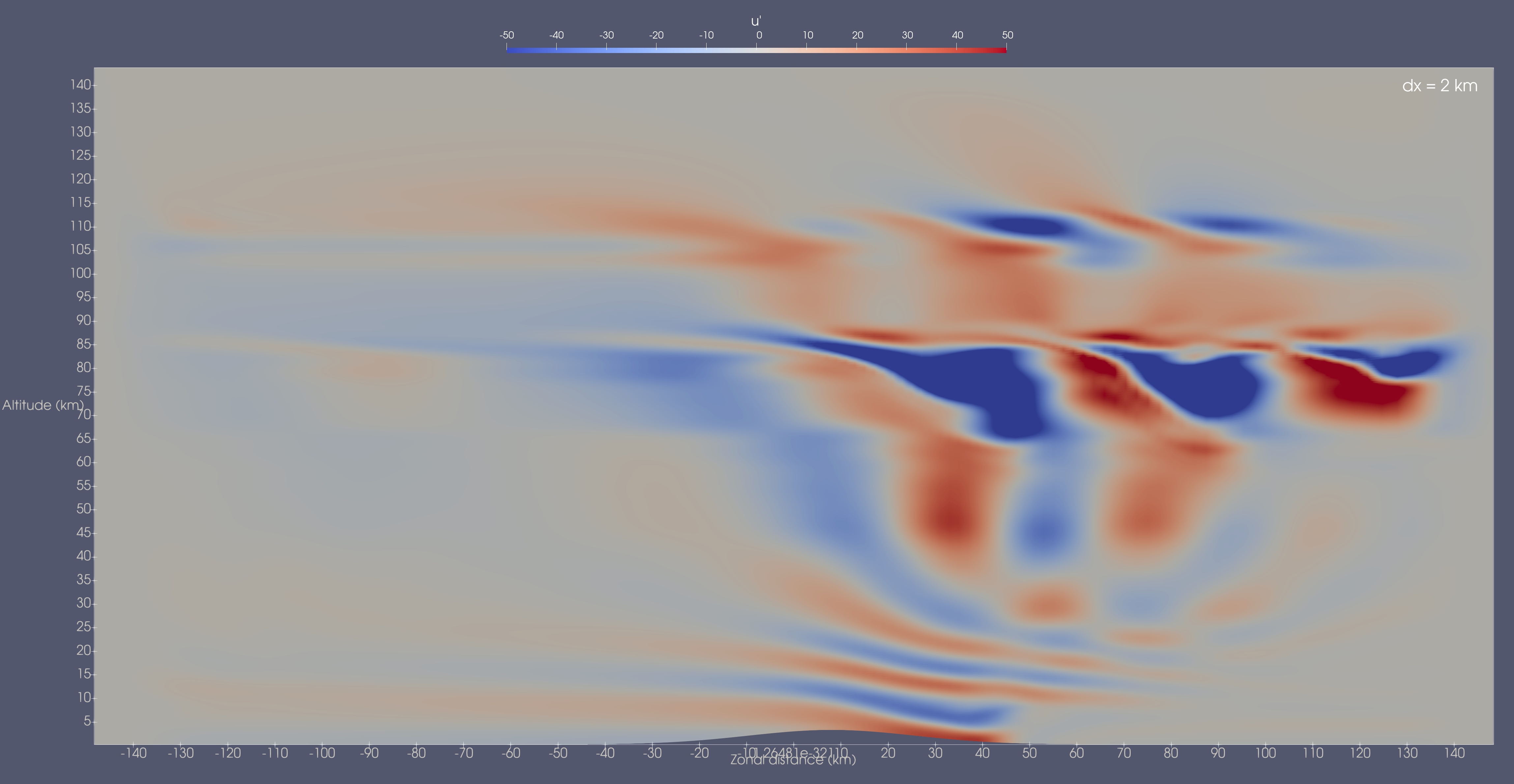
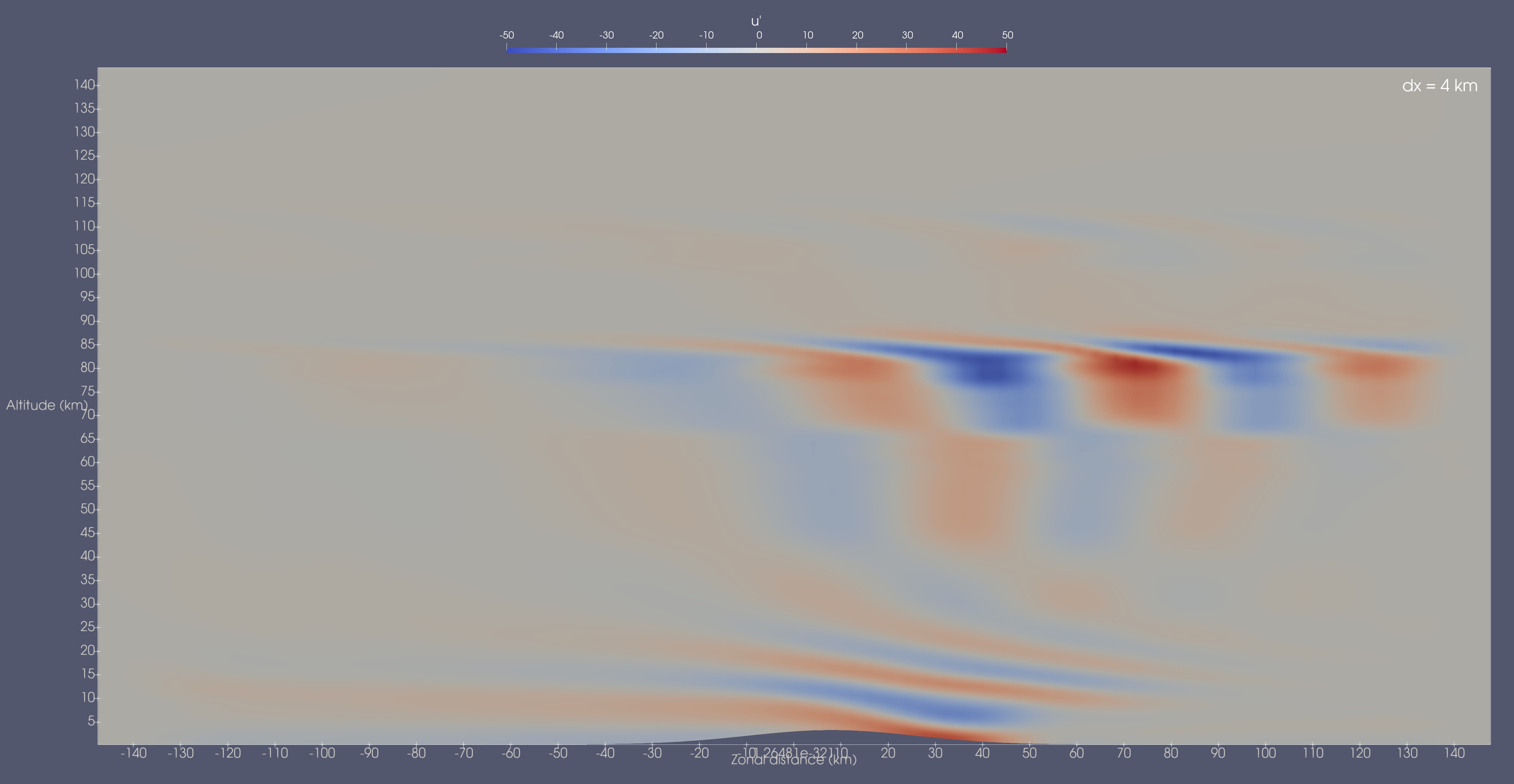
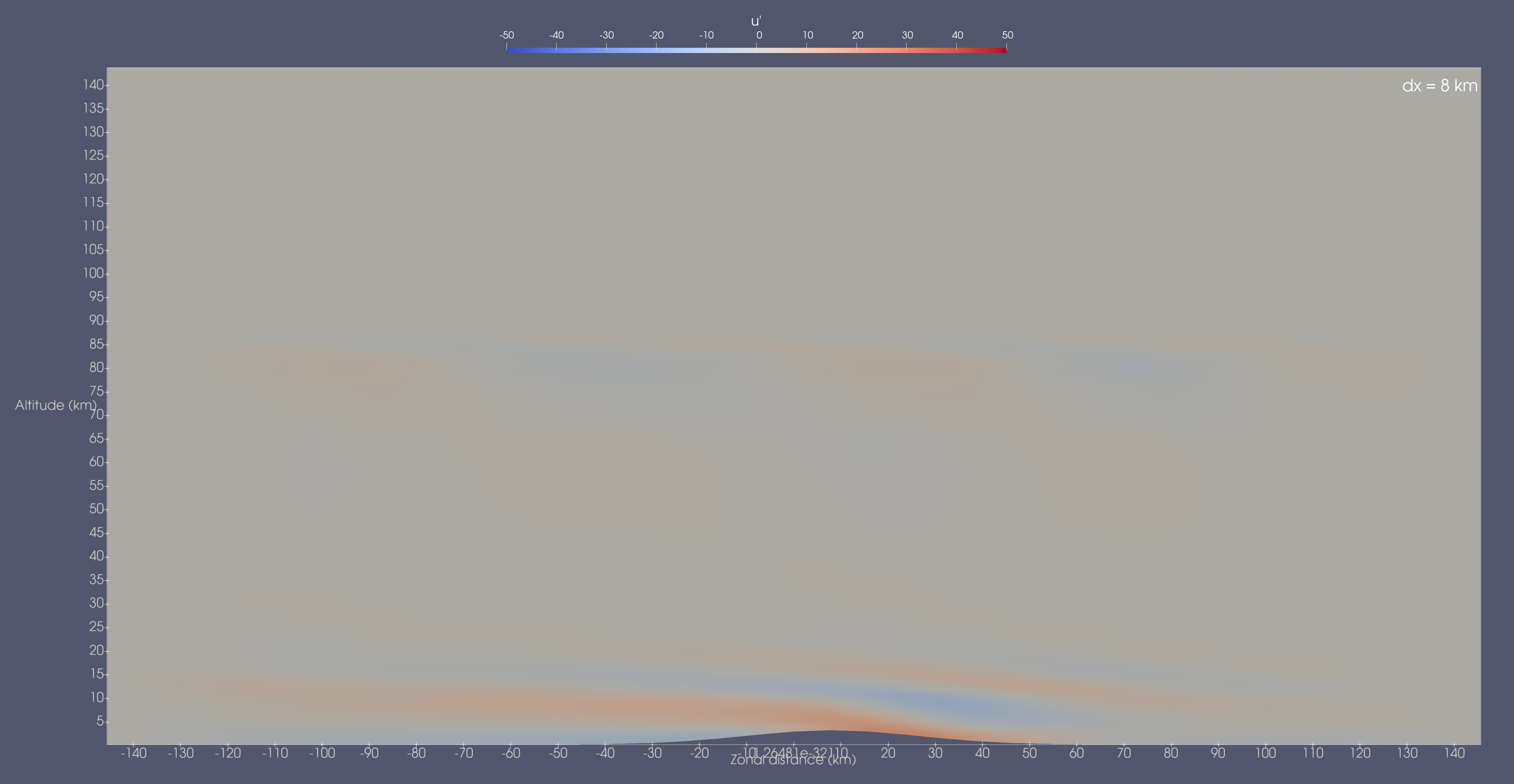
While there are some noticeable differences between the 1 and 2 km resolution cases, the overall wave pattern and strength is quite comparable. By stark contrast, the 2 and 4 km resolution cases do not compare well at all. The wave strength is much lower in the 4 km case and the overall wave pattern is also quite different with less amplification near the near critical level at 83 km and virtually no wave activity above it. The 8 km case continues this trend with very weak waves present only near the surface.
The drop in wave amplitude with deceasing resolution is shown quite well in the following plot of the u' streamwise spectra taken at an altitude of 18 km.
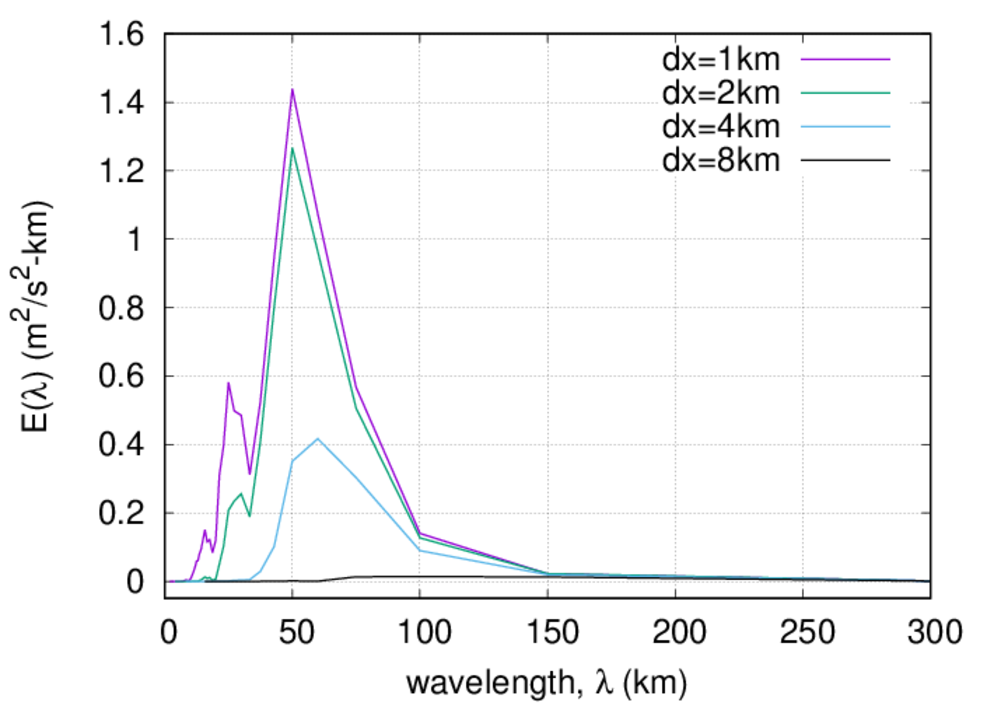
Consistent with the color images above, the 1 and 2 km resolution cases have comparable spectra with and energy peak at λ=50 km. The peak is broadened and shifts to λ=60 km for the 4 km case and the amplitude (square measure) is reduced by a factor of 3.5. The 8 km case shows negligible wave amplitude at 18 km.
These simulations were conducted in a rather controlled environment where the terrain is well-resolved in all cases and where the vertical mesh spacing, the time step, filter value, and sponge parameters were identical for all runs. Since the runs only go up to the time of late instability, all were also run without a turbulence model. This leaves just the zonal mesh spacing as the only variable. According to the 1 km case spectra, the dominant wavelength is 50 km, with sub-harmonic peaks at 25 and 12.5 km. While all of these peaks can be represented on the 4 km mesh (Nyquist scale 8 km), There will be considerable phase error at these scales. An effective way to characterize the phase error is in terms of the number of grid points per wavelength (points per wave or PPW). Considering the dominant mode at 50 km, the 1, 2, 4, and 8 km meshes have PPWs of 50, 25, 12.5, and 6.25. The first and second sub-harmonics have PPWs 1/2 and 1/4 of these values. Since our scheme is 2nd order accurate, the errors grow rapidly as the PPW parameter decreases. This behavior is shown in the following plot.
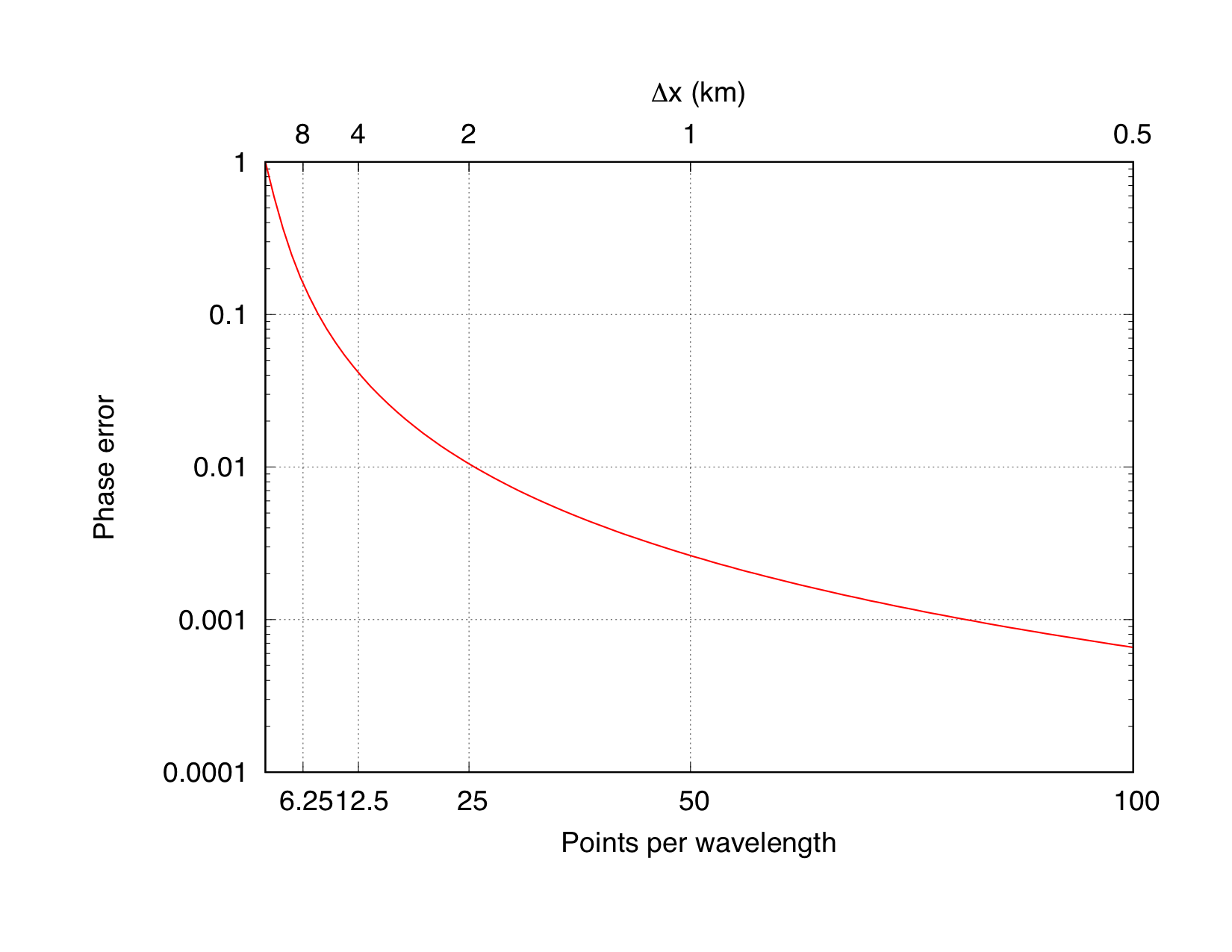
With the scheme being 2nd order, the error increases by a factor of 4 when the resolution is cut in half. We see that the 2 km resolution case has a phase error of about 1%, but this grows to 4 and 16% as the mesh is coarsened to 4 and 8 km. Since the gravity wave field is very sensitive to phase error, the solution degrades rapidly as the error increases. This observation is consistent with the heuristic requirement of PPW ≥ 40 that we have used previously to set the mesh spacing.
As the plot below shows, one symptom of the phase error appears to be a reduction in the vertical group velocity.
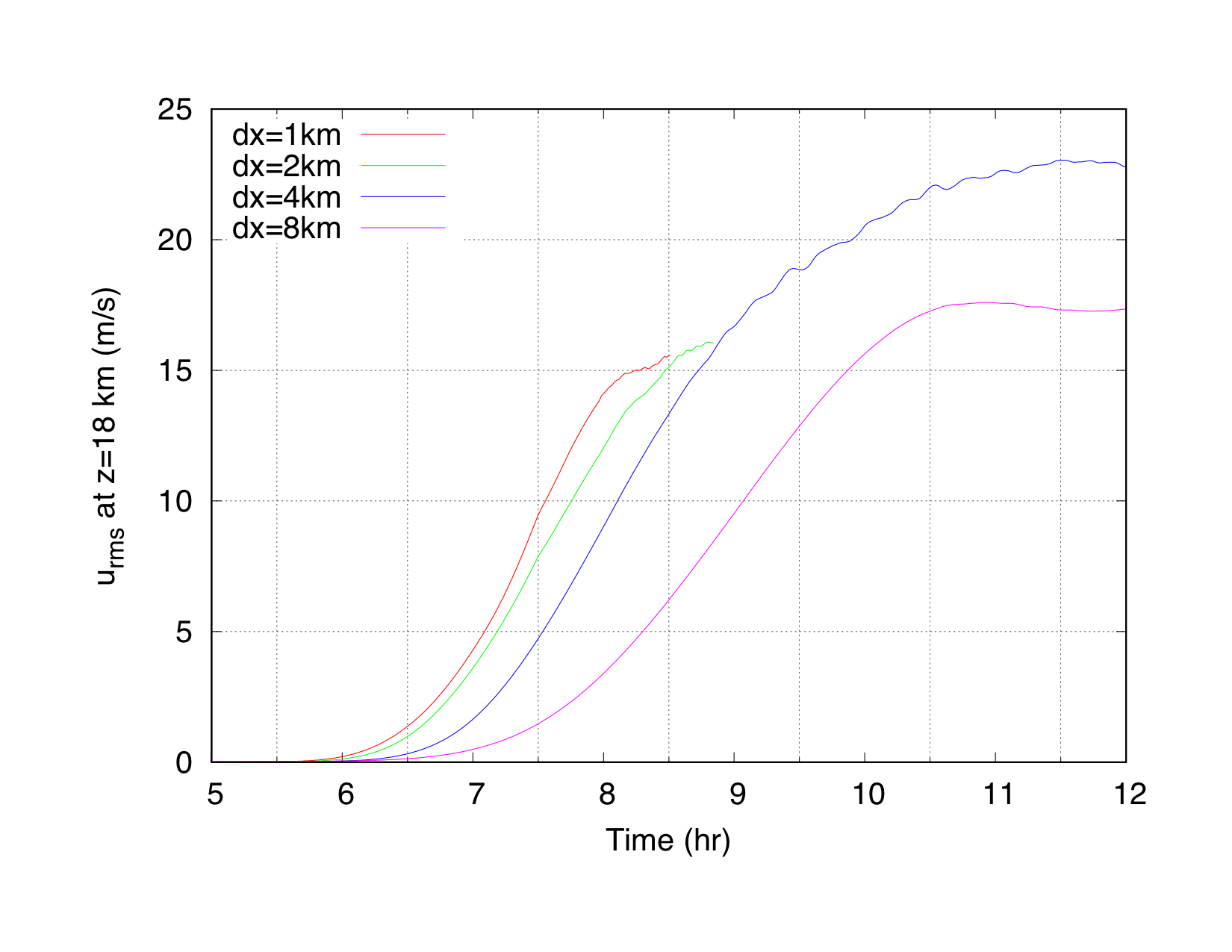
Here u_rms at an altitude of 18 km is plotted as a function of time for the various horizontal resolutions. Although the wind forcing is identical in all cases, there is an increasing delay in the wave activity at z=18 km as the mesh is coarsened. The 1km and 2km cases produce strong turbulence aloft after a time of 7.5 hr and also a tendency toward weak turbulence at an altitude of 13 km. These cases ultimately blow up when run in 2D and thus are only shown out to a time of about 8 hrs. The rms values in both of these cases show signs of leveling off, which would be consistent with a time-shifted rendition of the wind forcing profile, accounting for the time required for the wave packet to propagate to 18 km. The 4 and 8 km cases can be run much further in time and these show increasing time delays.
A second symptom of phase error is a mis-representation of the horizontal wavelength. The following plot illustrates this where the spectrum for the 8 km case at z=18 km is plotted at a time of 8.5 hr.
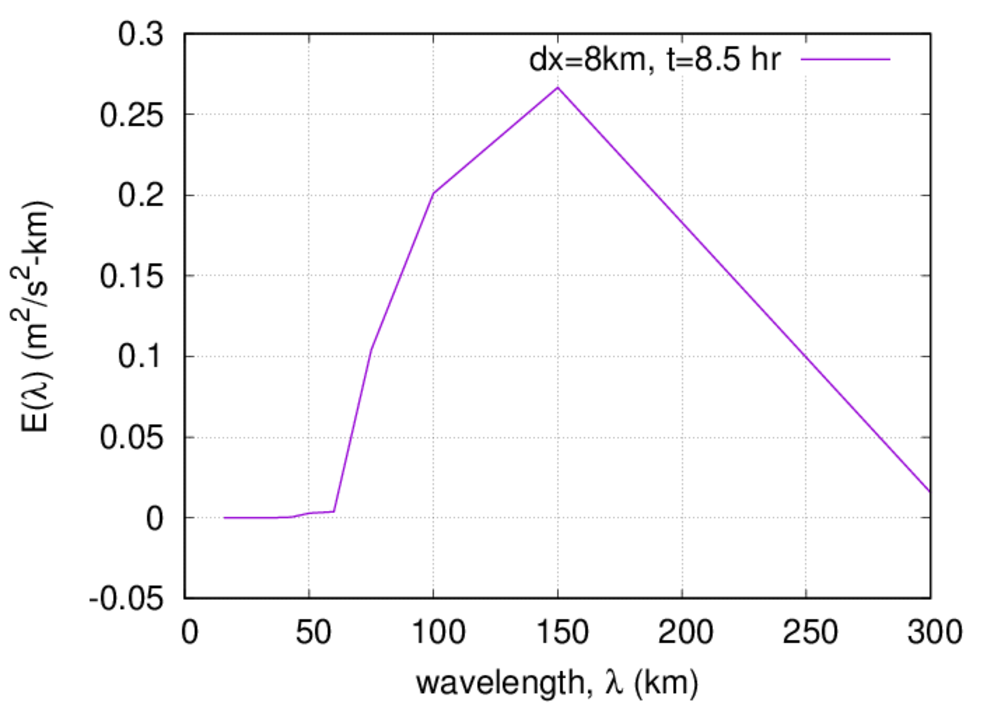
Here it is clear that the peak energy has been shifted all the way to λ=150 km. The shift in wavelength, coupled with the time shift, results in a high-altitude anomaly for the 8 km case at a time of 8 hrs (show in Figures 6 and 7 of the part 2 paper). Shortly before this time the leading edge of the retarded and elongated wave packet had encountered the near critical level at 83 km and critical level at 115 km. Being transient in nature, the leading edge of the packet can cross the critical levels. Reflections are also minimized due to the grossly exaggerated horizontal wavelength. The net result is a brief period where transient waves are observed at 150 and 180 km. To a lesser extent, transient waves are also seen at these altitudes in the better resolved cases, but they are weaker and appear at times earlier than 8 hr.
As discussed below, the results show that the wave strength evolves with an increasing time delay as the mesh is coarsened, and the energy peak moves to larger horizontal scale. The time delay results in smaller wave amplitudes at a given time as the mesh is coarsened. These effects become more pronounced as the mesh becomes very coarse, showing a large drop in wave amplitude (for a fixed time) when moving from 2 to 4 km spacing. Some evidence is provided to suggest that the precipitous drop in wave amplitude for the 4 and 8 km cases is caused by the rapid increase in phase error as the wave is resolved by a small number of grid points per wave length.
Shown below are the zonal velocity perturbations at 7.5 hr for the 4 different mesh resolutions.




While there are some noticeable differences between the 1 and 2 km resolution cases, the overall wave pattern and strength is quite comparable. By stark contrast, the 2 and 4 km resolution cases do not compare well at all. The wave strength is much lower in the 4 km case and the overall wave pattern is also quite different with less amplification near the near critical level at 83 km and virtually no wave activity above it. The 8 km case continues this trend with very weak waves present only near the surface.
The drop in wave amplitude with deceasing resolution is shown quite well in the following plot of the u' streamwise spectra taken at an altitude of 18 km.

Consistent with the color images above, the 1 and 2 km resolution cases have comparable spectra with and energy peak at λ=50 km. The peak is broadened and shifts to λ=60 km for the 4 km case and the amplitude (square measure) is reduced by a factor of 3.5. The 8 km case shows negligible wave amplitude at 18 km.
These simulations were conducted in a rather controlled environment where the terrain is well-resolved in all cases and where the vertical mesh spacing, the time step, filter value, and sponge parameters were identical for all runs. Since the runs only go up to the time of late instability, all were also run without a turbulence model. This leaves just the zonal mesh spacing as the only variable. According to the 1 km case spectra, the dominant wavelength is 50 km, with sub-harmonic peaks at 25 and 12.5 km. While all of these peaks can be represented on the 4 km mesh (Nyquist scale 8 km), There will be considerable phase error at these scales. An effective way to characterize the phase error is in terms of the number of grid points per wavelength (points per wave or PPW). Considering the dominant mode at 50 km, the 1, 2, 4, and 8 km meshes have PPWs of 50, 25, 12.5, and 6.25. The first and second sub-harmonics have PPWs 1/2 and 1/4 of these values. Since our scheme is 2nd order accurate, the errors grow rapidly as the PPW parameter decreases. This behavior is shown in the following plot.

With the scheme being 2nd order, the error increases by a factor of 4 when the resolution is cut in half. We see that the 2 km resolution case has a phase error of about 1%, but this grows to 4 and 16% as the mesh is coarsened to 4 and 8 km. Since the gravity wave field is very sensitive to phase error, the solution degrades rapidly as the error increases. This observation is consistent with the heuristic requirement of PPW ≥ 40 that we have used previously to set the mesh spacing.
As the plot below shows, one symptom of the phase error appears to be a reduction in the vertical group velocity.

Here u_rms at an altitude of 18 km is plotted as a function of time for the various horizontal resolutions. Although the wind forcing is identical in all cases, there is an increasing delay in the wave activity at z=18 km as the mesh is coarsened. The 1km and 2km cases produce strong turbulence aloft after a time of 7.5 hr and also a tendency toward weak turbulence at an altitude of 13 km. These cases ultimately blow up when run in 2D and thus are only shown out to a time of about 8 hrs. The rms values in both of these cases show signs of leveling off, which would be consistent with a time-shifted rendition of the wind forcing profile, accounting for the time required for the wave packet to propagate to 18 km. The 4 and 8 km cases can be run much further in time and these show increasing time delays.
A second symptom of phase error is a mis-representation of the horizontal wavelength. The following plot illustrates this where the spectrum for the 8 km case at z=18 km is plotted at a time of 8.5 hr.

Here it is clear that the peak energy has been shifted all the way to λ=150 km. The shift in wavelength, coupled with the time shift, results in a high-altitude anomaly for the 8 km case at a time of 8 hrs (show in Figures 6 and 7 of the part 2 paper). Shortly before this time the leading edge of the retarded and elongated wave packet had encountered the near critical level at 83 km and critical level at 115 km. Being transient in nature, the leading edge of the packet can cross the critical levels. Reflections are also minimized due to the grossly exaggerated horizontal wavelength. The net result is a brief period where transient waves are observed at 150 and 180 km. To a lesser extent, transient waves are also seen at these altitudes in the better resolved cases, but they are weaker and appear at times earlier than 8 hr.