Animation of mode 2 soliton displacement
Animation of mode 2 soliton surface current
The movie files below show the motion of the soliton as well at its induced surface current. The phase speed was measured at 13.2 cm/sec and the full visual pulse width is about 600 cm. This compares with 4.2 cm/sec and ~100 cm for the mode 2 wave. Aside from these quantitative differences, the surface current is qualitatively almost identical for the mode 2 and mode 1 waves. This is expected from KDV theory, since the horizontal structure is independent of the mode number. The latter only affects the vertical structure of the wave. The surface current shows the emergence of a sequence of trailing waves late into the simulation. These appear to be mode 1 solitons with alternating sense (depression, elevation).
Study 2: Mode 1 Soliton From Lab Tests
The second study involves the simulation of a mode 1 soliton with the same initial displacement amplitude as the mode 2 case described above. This soliton has a much larger pulse width and much greater phase speed. Although the KDV solution solution provides a much better initial condition in this case, the same purification procedure described for the mode 2 case was also employed here. Due two the enlarged pulse width and phase speed, the simulation domain needed to be increased significantly over what was used for the mode 2 simulation.The movie files below show the motion of the soliton as well at its induced surface current. The phase speed was measured at 13.2 cm/sec and the full visual pulse width is about 600 cm. This compares with 4.2 cm/sec and ~100 cm for the mode 2 wave. Aside from these quantitative differences, the surface current is qualitatively almost identical for the mode 2 and mode 1 waves. This is expected from KDV theory, since the horizontal structure is independent of the mode number. The latter only affects the vertical structure of the wave. The surface current shows the emergence of a sequence of trailing waves late into the simulation. These appear to be mode 1 solitons with alternating sense (depression, elevation).
Animation of mode 1 soliton streamwise velocity
Animation of mode 1 soliton displacement
Animation of mode 1 soliton surface current
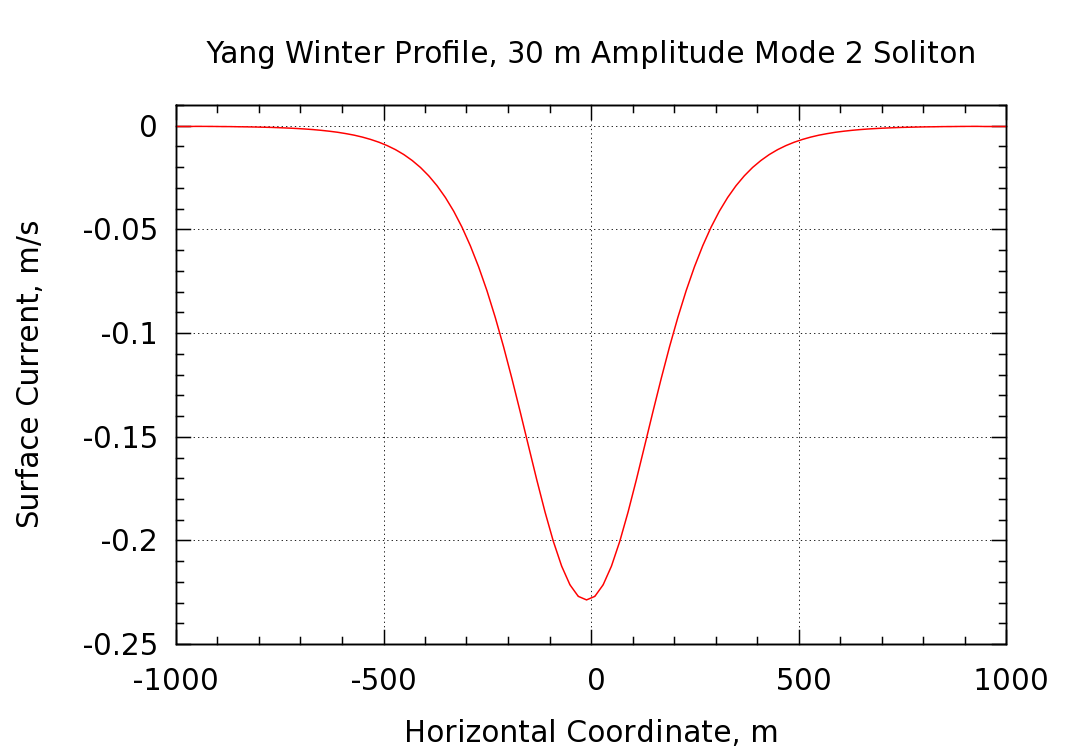
The simulation was first initialized with the shallow water water KDV solution. Since this solution is only approximate, the purification procedure described in the Study 1 discussion above was used to arrive at an initial condition that is a much better solution to the Euler equations. The displacement amplitude changes slightly during the purification procedure, making it necessary to iterate in order to arrive at the improved initial condition with the desired amplitude. Only one iteration cycle was undertaken and thus the target amplitude was not hit exactly. The simulation described below has a displacement amplitude of 29.75 m whereas 30 m was desired. Starting from the improved initial condition, the simulation was run for a period of time corresponding to 2.5 hours of physical time. During this time, the soliton propagates a distance of 6,392 m, giving a phase speed of 0.710 m/s. The surface current profile is shown below. The soliton is propagating to the right (positive x direction) and the surface current is to the left (negative x direction)
An animation of the surface current evolution can be viewed by clicking the image below
The soliton propagates at nearly constant speed and amplitude and the surface current follows suit. A very slight undular tail develops and propagates to the left behind the main surface current pulse.
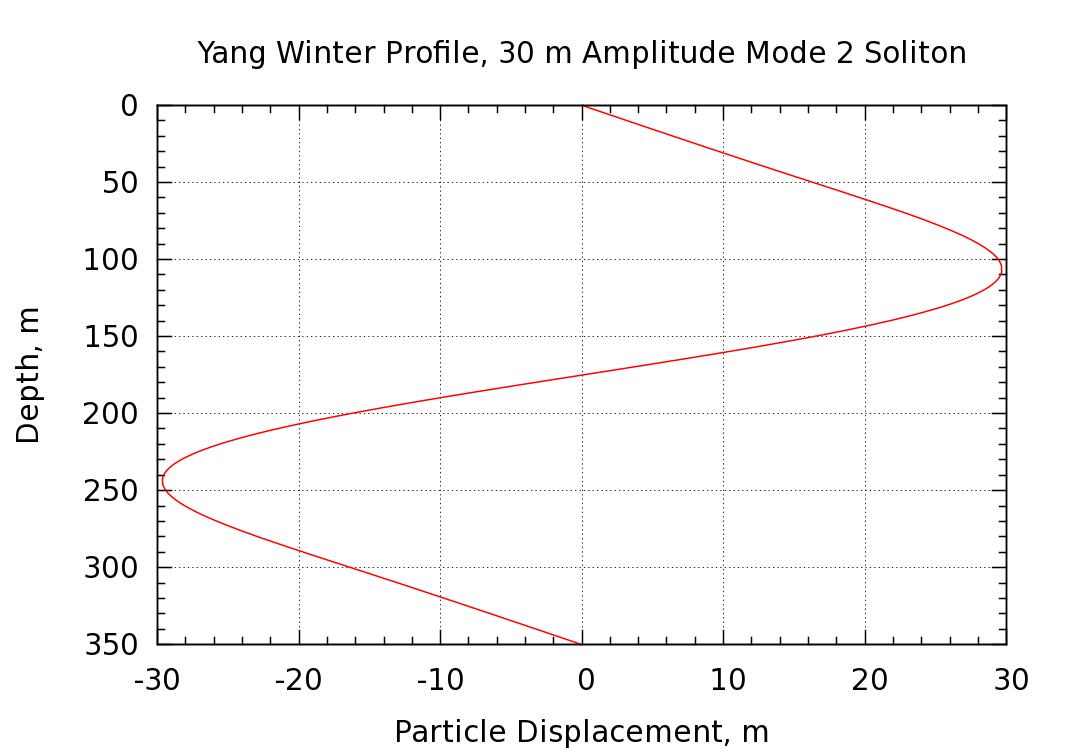
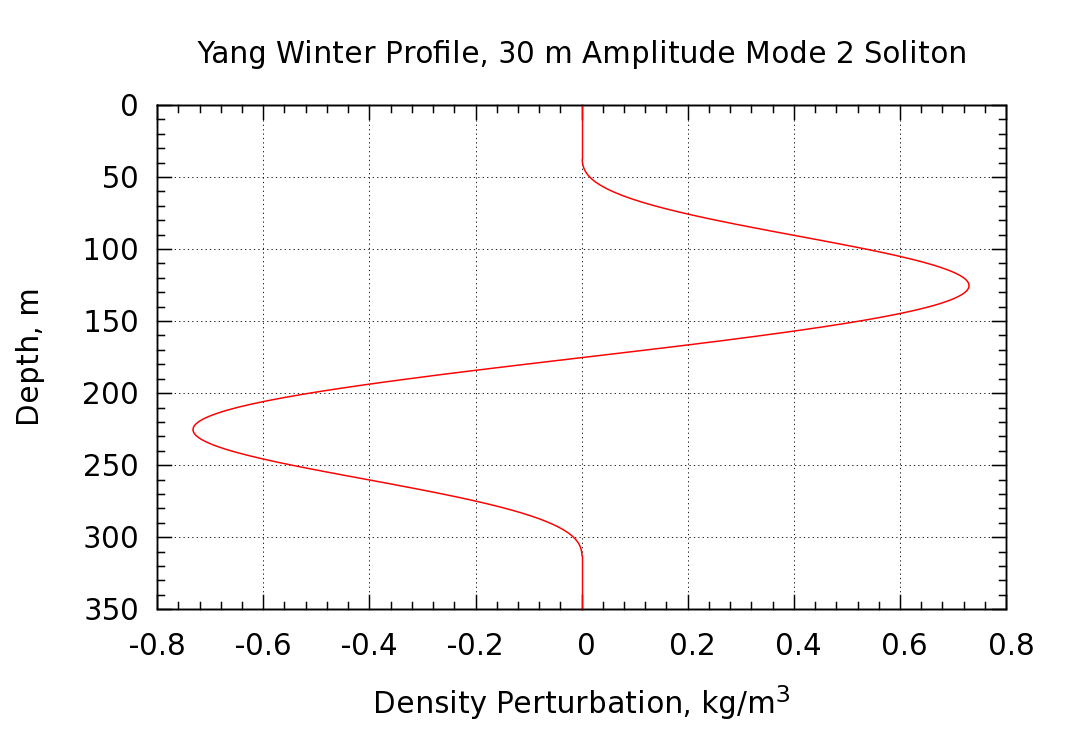
The particle vertical displacement and density perturbation profiles at the center of the soliton (where the displacements are maximized) are shown in the following two plots.
Contours of constant density are shown in the plot below.
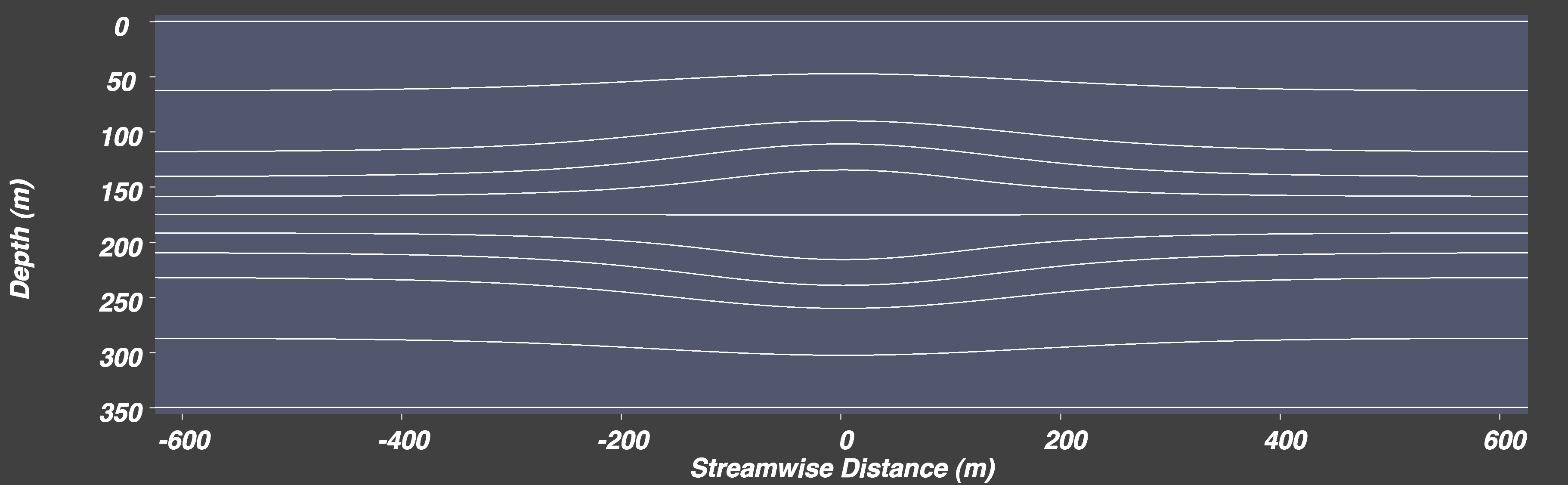
This plot illustrates that the mode 2 soliton displaces fluid upward above the soliton center and downward below the center. This action is brought about by a pair of counter-rotating vortices as illustrated in the following plot showing the vorticity contours. The soliton is propagating to the right, and thus there is an apparent flow from the left in a frame of reference fixed to the soliton center. The combined flow of the uniform stream plus the "doublet" yields streamlines that are deflected symmetrically above and below just as if a solid body were present in the flow. The density can be thought of as a passive traces under the Boussinesq approximation since it is simply related to the temperature (and/or salinity). Thus the lines of constant density are effectively streamlines, which helps us visualize the flow created by the "doublet" and uniform stream.

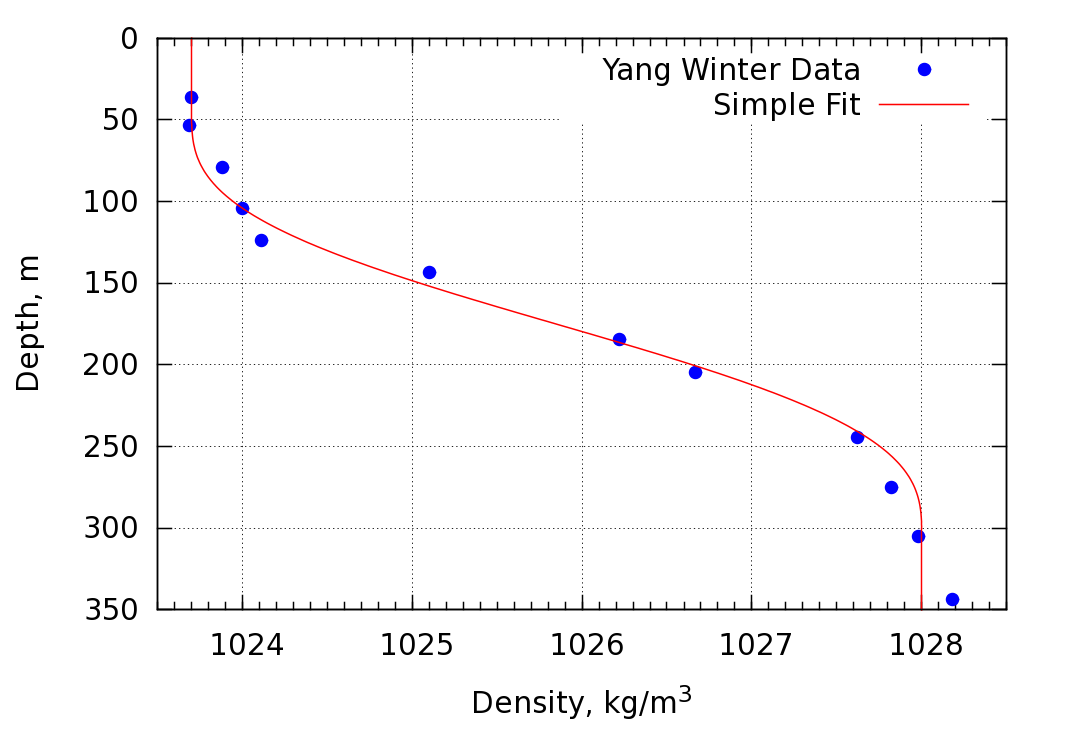
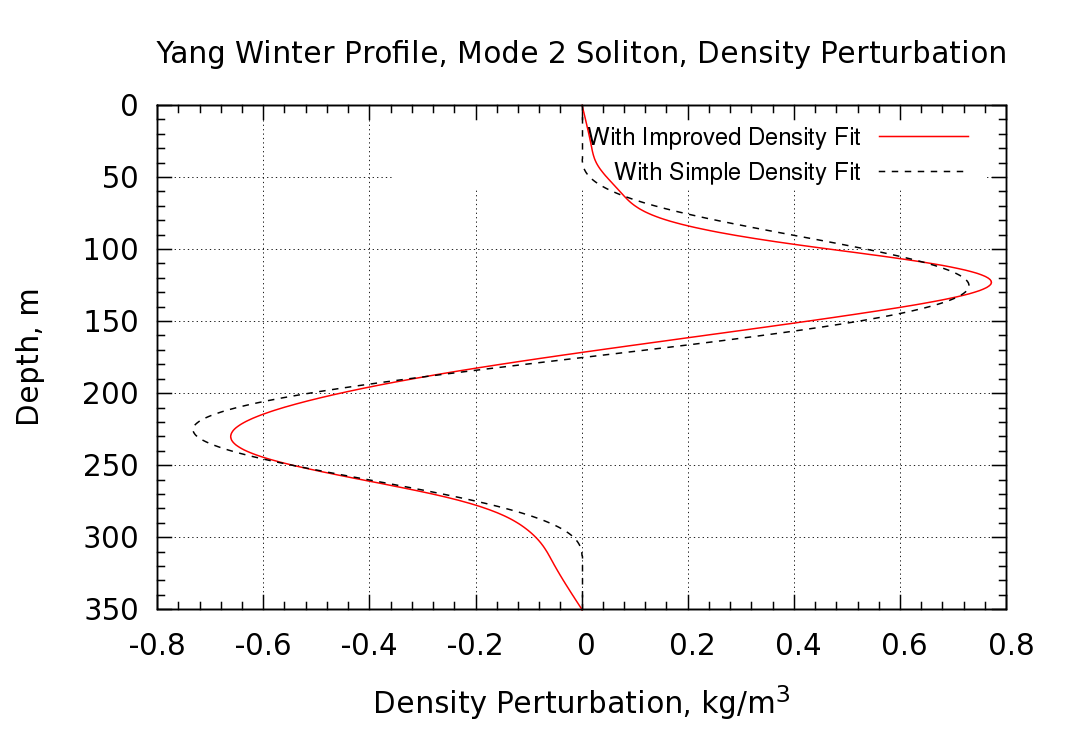
The largest difference between the simple and improved fit occur near the top and bottom edges of the profile. The improved fit is also slightly asymmetric about the midpoint at ~175 m.
The simulation was run using the purified initial condition procedure as in Study 3. The target amplitude of 30 m was achieved almost exactly.
The main difference between the cases with simple and improved density fit is asymmetries in the displacement field. This effect is shown in the figure below where the displacements are compared.
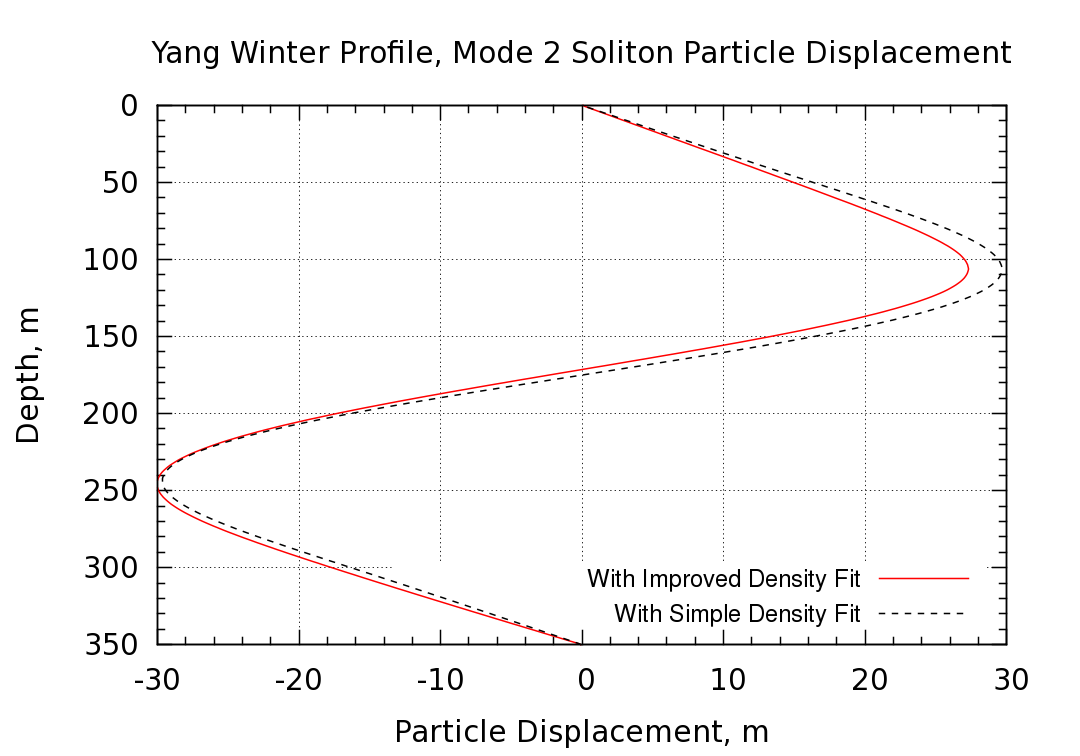
The depths for maximum displacement are practically unchanged. The only significant difference between the two displacement fields is the asymmetry which results in a smaller maximum displacement (+27.3 m) on the top half of the profile as compared with the bottom (-30.0 m). Unfortunately this is opposite to the trend in the measurements where a displacement of 30 +/- 18 m at 75 m depth and -26 +/- 16 m at 240 m depth were reported. Thus the improved fit to the density profile does not seem to improve the comparison with the field measurements.
The asymmetry also shows up in the perturbation density profile as shown below.
The simulation was run for a a period of time corresponding to 2.5 hours of physical time. During this time, the soliton propagates a distance of 6,335 m, giving a phase speed of 0.704 m/s. The surface current profile is shown below. The soliton is propagating to the right (positive x direction) and the surface current is to the left (negative x direction)
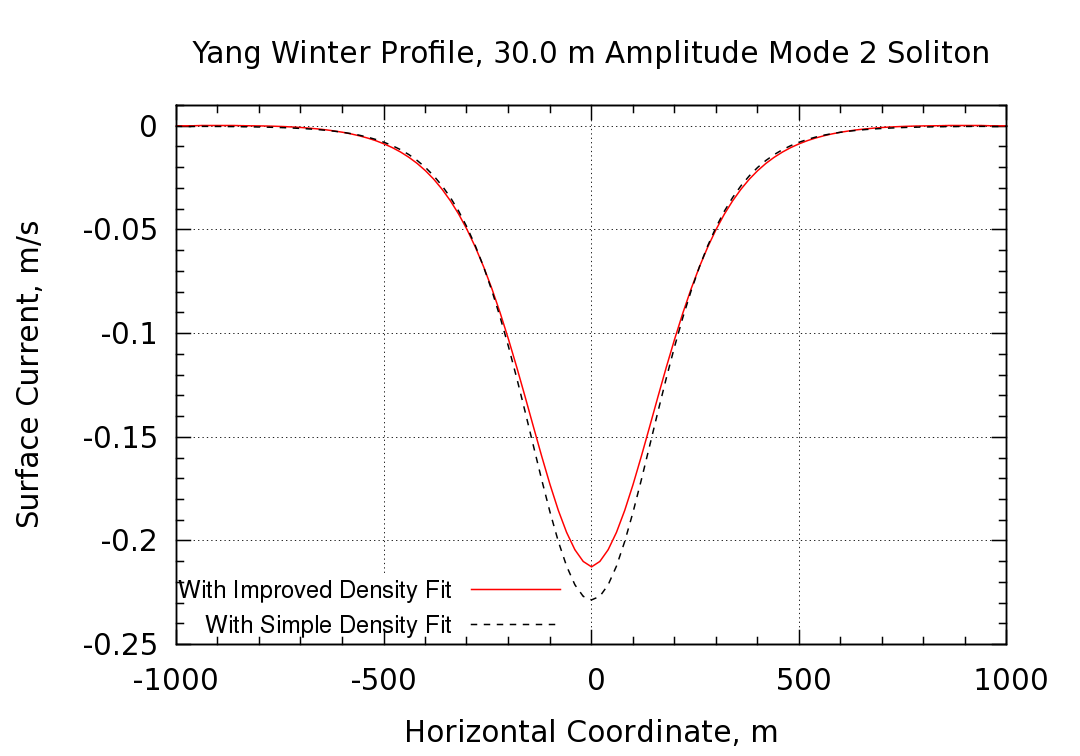
The shape of the current profile is almost unchanged by the details of the density fit. The maximum amplitude does change, mainly in response to the top-to-bottom asymmetries that result in lower displacements on the upper half of the profile. It is likely that if the simulation were redone targeting a 30 m displacement on the upper half of the profile, the surface currents between the two cases would be nearly identical.
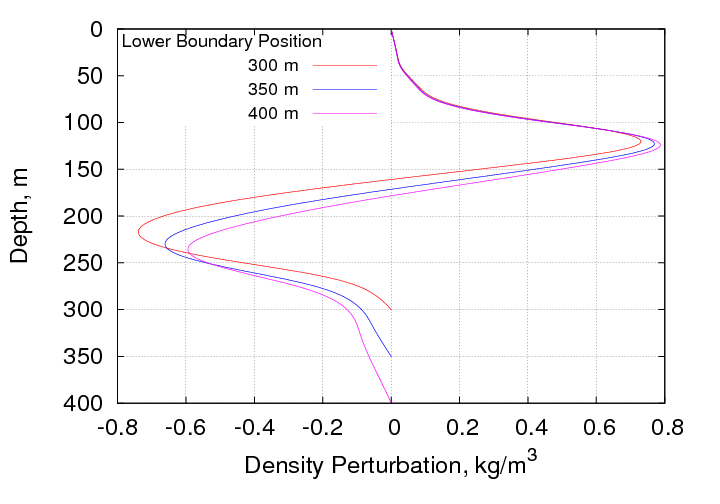
Simulations were run with lower boundaries placed at depths of 400 and 450 m. As shown below, the main effect of moving the lower boundary downward is to displace the position of maximum negative displacement to greater depth, while leaving the position of the position maximum relatively unchanged. This actually worsens the agreement with the measurements. Since moving the lower boundary downward had the wrong effect, a case was also run by moving it upward to a depth of 300 m. The results from simulations with the lower boundary placed at 300, 350 and 400 m are shown below.
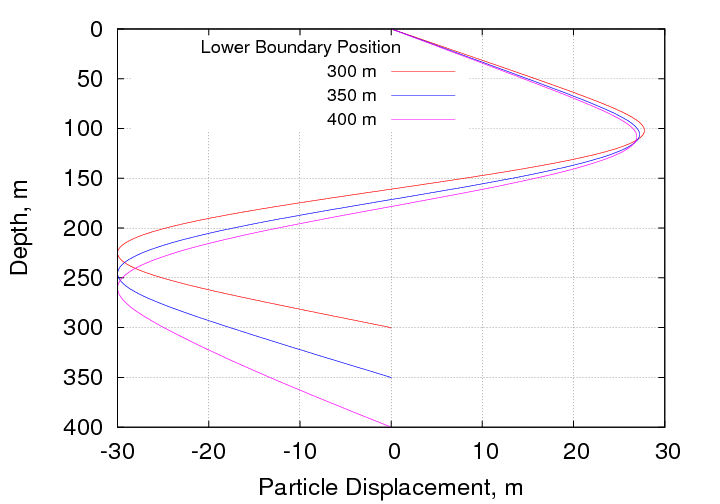
The trend is very clear; the positions of both the positive and negative displacement maxima follow the position of the lower boundary, but the effect is much greater for the negative maximum. The net result is that the position of positive maximum is very little changed, while the position of the negative maximum is only in good agreement with the measurements if a lower boundary position of 350 m is used. The asymmetry between the positive and negative maxima is also fairly insensitive to the boundary position and, as a result, this discrepancy with the measurements is not improved by moving the lower boundary either.
Comparison of the density profiles is shown below.
The resulting displacement profile is compared with the result of the fully-smoothed density profile in the following plot.
The reduced smoothing is seen to move the displacement field in the wrong direction by increasing the depth for the maximum positive displacement and reducing its value.
All three cases shown above produce displacement maxima close to the 75 and 240 m depths quoted by Yang. The asymmetries between the positive and negative maxima could not be reproduced, however. One common feature in the cases shown above is that all of them require a non-zero displacement on the ocean surface. Since these displacement are in the 15-18 m range there is little chance that any of these cases are realizable.
Initially simulations were run at 48 m amplitude, which is at the upper end of the observed range. These simulations lead to instabilities that appear to be of the wave breaking type. After some trial and error it was determined that instabilities would occur for amplitudes greater than about 40 m. Thus we chose 40 m as our target amplitude, as this is slightly below the instability threshold.
The density profile was fit with the simple symmetric trigonometric function as discussed in Study 3 above. The purification procedure discussed in Study 1 was used to produce an initial condition that is a good solution to the Euler equations. Starting from the improved initial condition, the simulation was run for a period of time corresponding to 2.5 hours of physical time. During this time, the soliton propagates a distance of 6,674 m, giving a phase speed of 0.742 m/s. The surface current profile is shown below. The soliton is propagating to the right (positive x direction) and the surface current is to the left (negative x direction)
An animation of the surface current evolution can be viewed by clicking the image below
The soliton propagates at nearly constant speed and amplitude and the surface current follows suit. A very slight undular tail develops and propagates to the left behind the main surface current pulse.
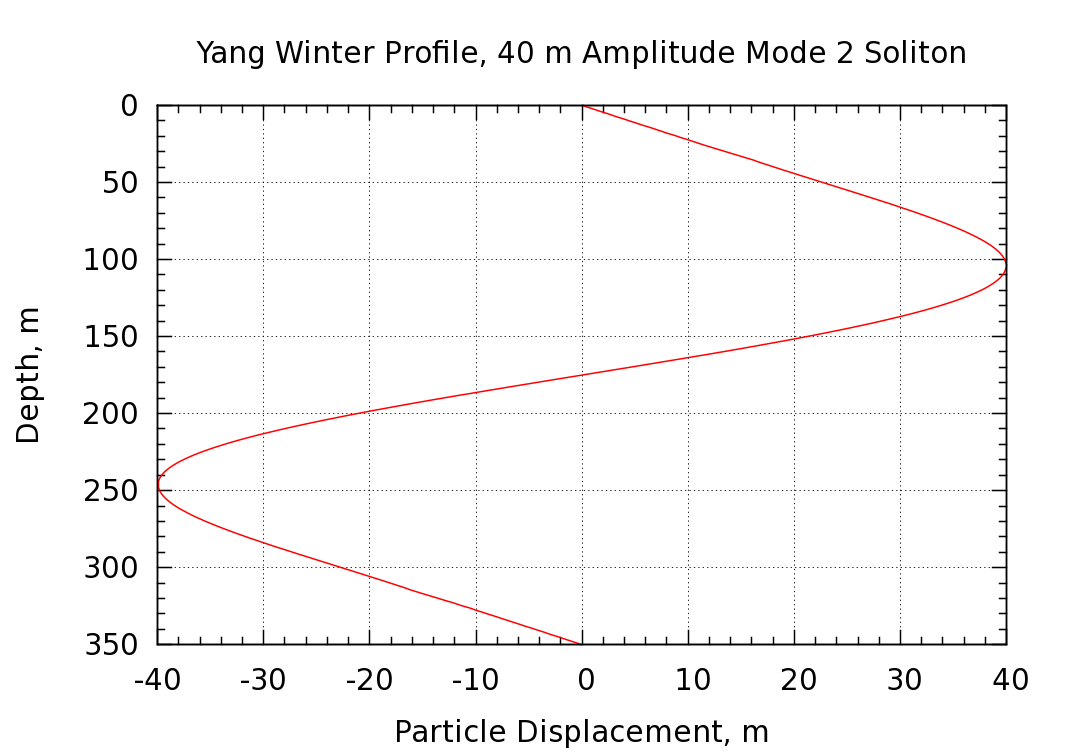
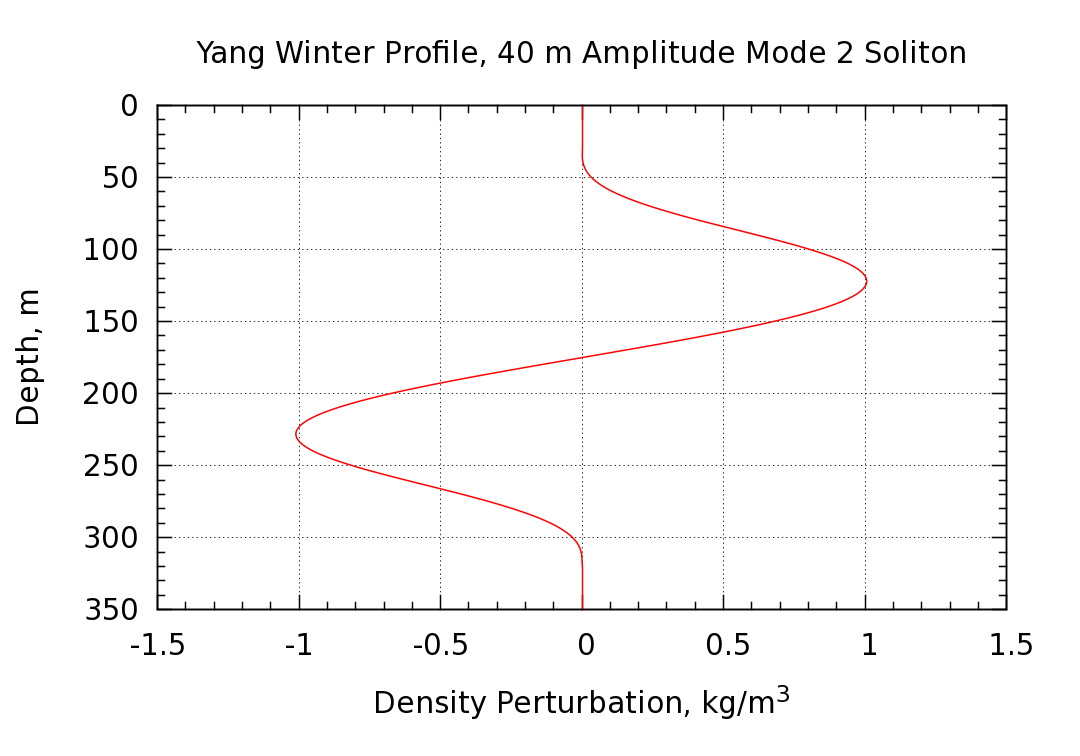
The particle vertical displacement and density perturbation profiles at the center of the soliton (where the displacements are maximized) are shown in the following two plots.
The density profile was fit with the simple symmetric trigonometric function as discussed in Study 3 above. The purification procedure discussed in Study 1 was used to produce an initial condition that is a good solution to the Euler equations. Starting from the improved initial condition, the simulation was run for a period of time corresponding to 2.5 hours of physical time. During this time, the soliton propagates a distance of 13,589 m, giving a phase speed of 1.510 m/s. The surface current profile is shown below. The soliton is propagating to the right (positive x direction) and the surface current is also to the right (positive x direction)
An animation of the surface current evolution can be viewed by clicking the image below
The surface current for the mode 1 wave is seen to develop a pronounced undular tail as time goes on. The tail is significantly large that it extracts energy from the main pulse, and thus the maximum suface current decreases in time. Since this behavior is rather different from the mode 2 wave (where almost no tail develops), several checks were performed to ensure that the mode 1 simulation is sound. The KDV solver which provides the initial condition is unified so that the only difference between computing a mode 1 and a mode 2 soliton is in solving the eigenvalue problem for the mode shape. Only mild transients appeare when the model 1 KDV solution is advanced in time in the Euler equation solver, indicating that the initial condition is sound. It was found that the extent to which an undular tail develops is dependent on the soliton amplitude. Mode 1 waves with amplitudes on the order of a few meters do not produce tails. Tails were observed for amplitudes greater than about 5 m, and become more pronounced as the amplitude is increased. Several references to undular tails were found via a google search and a few images of similar looking wave forms were spotted. Thus at this point it appears that the undular tail is a realistic characteristic of a large amplitude mode 1 wave.
The particle vertical displacement and density perturbation profiles at the center of the soliton (where the displacements are maximized) are shown in the following two plots.
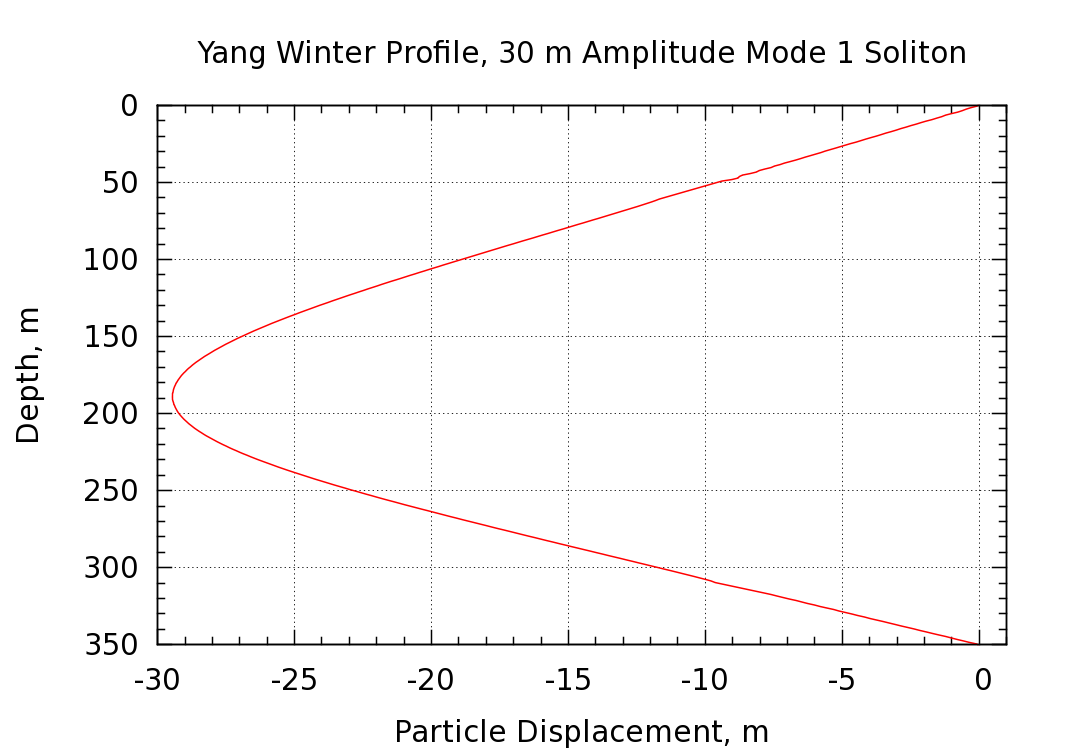
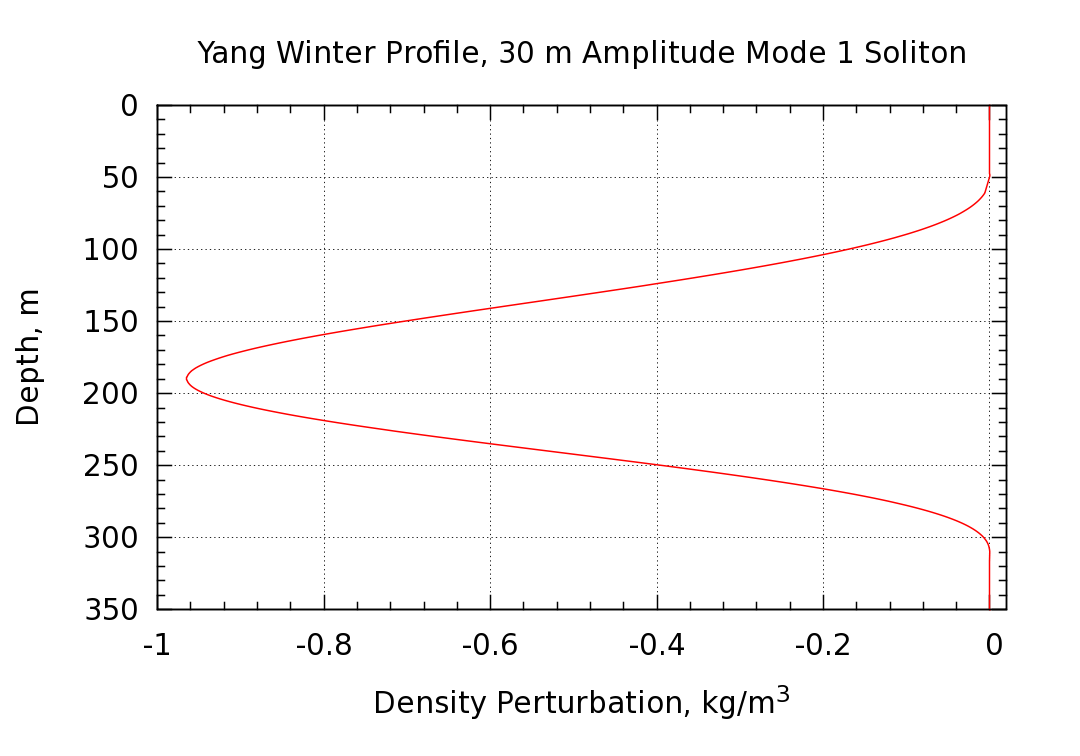
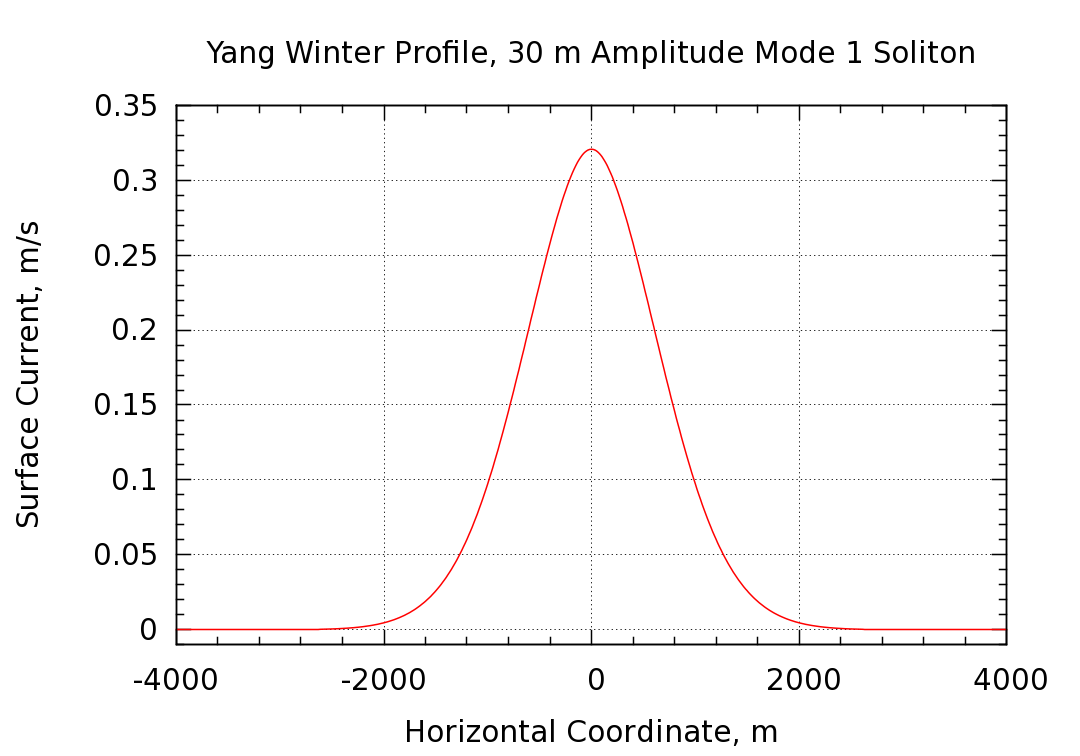
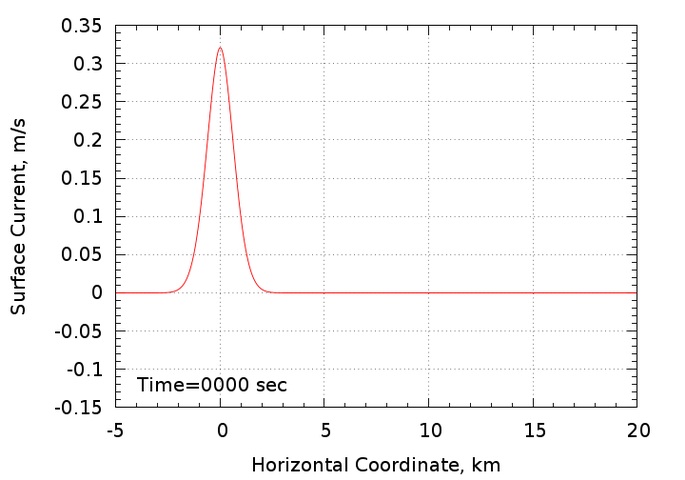
The simulation was first initialized with the shallow water water KDV solution. Since this solution is only approximate, the purification procedure described in the Study 1 discussion above was used to arrive at an initial condition that is a much better solution to the Euler equations. The displacement amplitude changes slightly during the purification procedure, making it necessary to iterate in order to arrive at the improved initial condition with the desired amplitude. Two iteration cycles were undertaken and thus the target amplitude was not hit exactly. The simulation described below has a displacement amplitude of 29.9 m whereas 30 m was desired. Starting from the improved initial condition, the simulation was run for a period of time corresponding to 4.17 hours of physical time. During this time, the soliton propagates a distance of 11,378 m, giving a phase speed of 0.759 m/s. The surface current profile is shown below. The soliton is propagating to the right (positive x direction) and the surface current is to the left (negative x direction)
Study 3: Mode 2 Soliton From Yang's Winter Density Profile
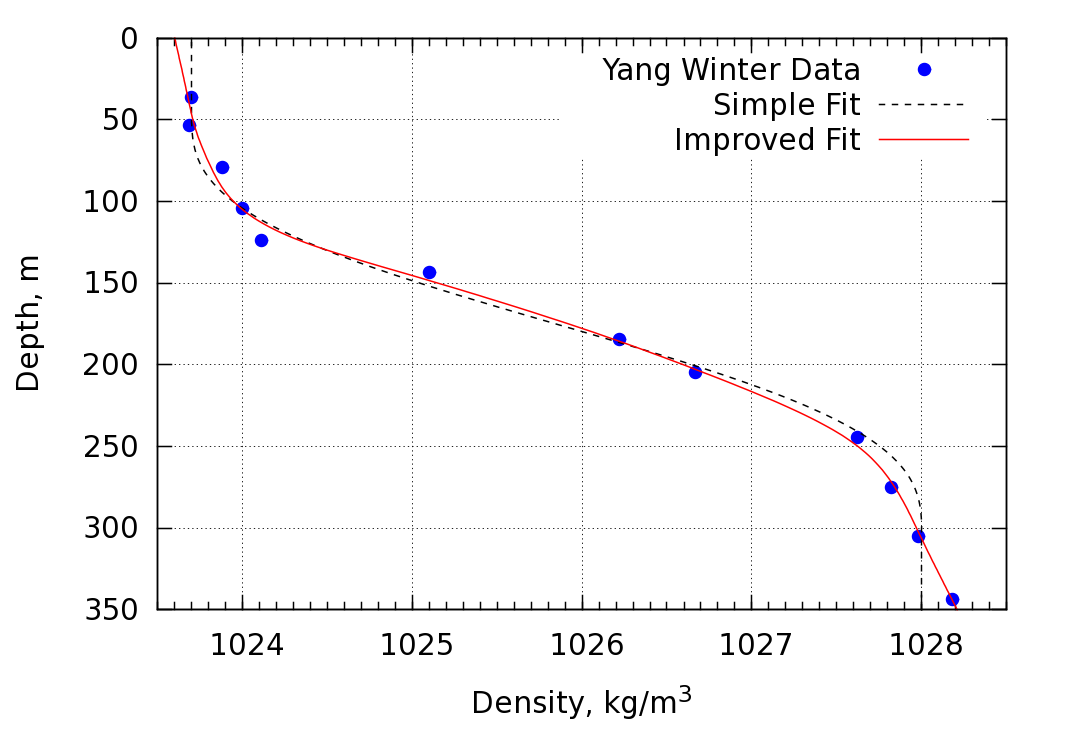
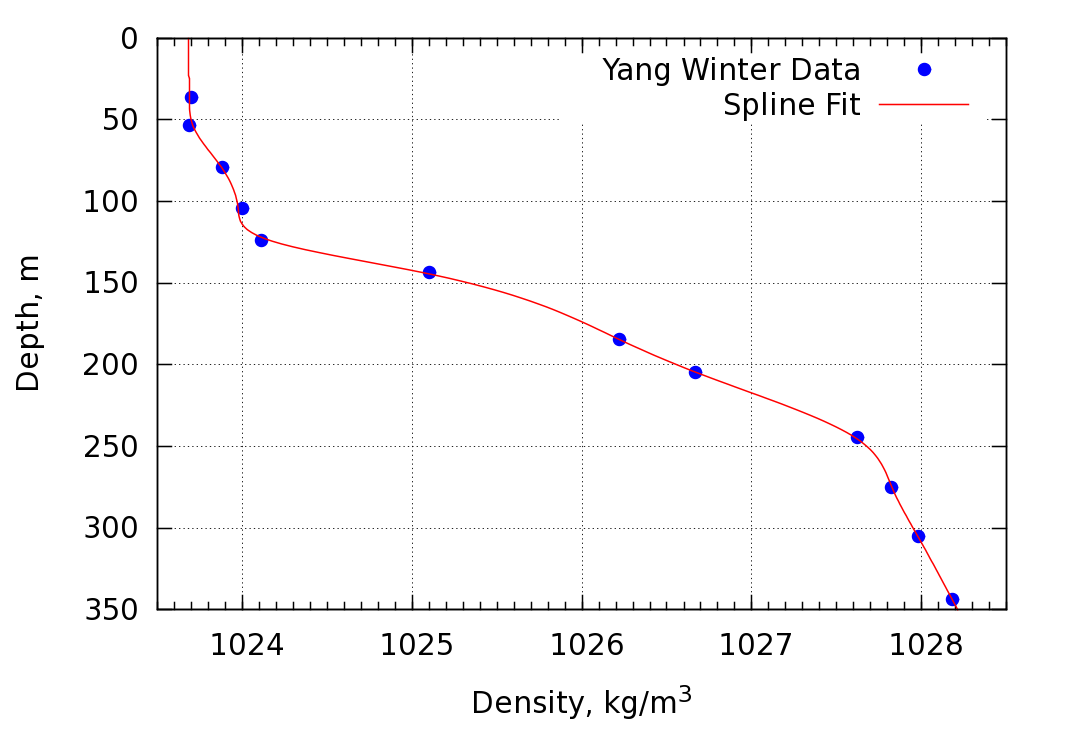
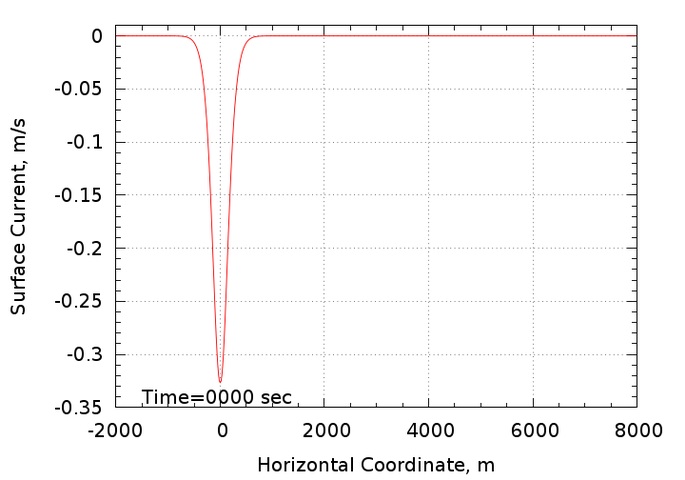
The third study involves the simulation of a mode 2 soliton with an amplitude of ~30 m propagating in the duct corresponding to the density profile in Yang's winter measurements. The data was curve-fit in order to provide a continuous density distribution to be used in the simulation. The fit is shown below
The simulation was first initialized with the shallow water water KDV solution. Since this solution is only approximate, the purification procedure described in the Study 1 discussion above was used to arrive at an initial condition that is a much better solution to the Euler equations. The displacement amplitude changes slightly during the purification procedure, making it necessary to iterate in order to arrive at the improved initial condition with the desired amplitude. Only one iteration cycle was undertaken and thus the target amplitude was not hit exactly. The simulation described below has a displacement amplitude of 29.75 m whereas 30 m was desired. Starting from the improved initial condition, the simulation was run for a period of time corresponding to 2.5 hours of physical time. During this time, the soliton propagates a distance of 6,392 m, giving a phase speed of 0.710 m/s. The surface current profile is shown below. The soliton is propagating to the right (positive x direction) and the surface current is to the left (negative x direction)

An animation of the surface current evolution can be viewed by clicking the image below

The soliton propagates at nearly constant speed and amplitude and the surface current follows suit. A very slight undular tail develops and propagates to the left behind the main surface current pulse.
The particle vertical displacement and density perturbation profiles at the center of the soliton (where the displacements are maximized) are shown in the following two plots.


Contours of constant density are shown in the plot below.

This plot illustrates that the mode 2 soliton displaces fluid upward above the soliton center and downward below the center. This action is brought about by a pair of counter-rotating vortices as illustrated in the following plot showing the vorticity contours. The soliton is propagating to the right, and thus there is an apparent flow from the left in a frame of reference fixed to the soliton center. The combined flow of the uniform stream plus the "doublet" yields streamlines that are deflected symmetrically above and below just as if a solid body were present in the flow. The density can be thought of as a passive traces under the Boussinesq approximation since it is simply related to the temperature (and/or salinity). Thus the lines of constant density are effectively streamlines, which helps us visualize the flow created by the "doublet" and uniform stream.

grid file for contour plots
vorticity data file for contour plots
density data file for contour plots
vorticity data file for contour plots
density data file for contour plots
Study 4: Attempts to improve the agreement between Mode 2 Soliton simulations and Yang's Winter measurements
Here we repeat the basic case of Study 3, but with small variations in parameters in an attempt to improve the agreement between the simulations and Yang's winter measurements. Study 3 produced a displacement amplitude with maxima at 105 and 245 m, but Yang reports observing maxima at 75 and 240 m. Furthermore Yang reports a maximum displacement of 30 +/- 18 m at 75 m depth and -26 +/- 16 m at 240 m depth, while the results of Study 3 are symmetric, giving displacements of 30 m at 105 m depth and -30 m at 245 m depth.4.1 Improved fit to Yang's Winter Density Profile
Study 3 used a very simple trigonometric function to fit Yang's measured winter density profile. Being symmetric about the mid-depth point, this profile naturally lead to symmetric displacement maxima and symmetric depths at which the maxima occur. Here we fit the density data accurately using a smoothed cubic spline. Smoothing was used since the data appear to contain measurement error. The improved fit is shown below
The largest difference between the simple and improved fit occur near the top and bottom edges of the profile. The improved fit is also slightly asymmetric about the midpoint at ~175 m.
The simulation was run using the purified initial condition procedure as in Study 3. The target amplitude of 30 m was achieved almost exactly.
The main difference between the cases with simple and improved density fit is asymmetries in the displacement field. This effect is shown in the figure below where the displacements are compared.

The depths for maximum displacement are practically unchanged. The only significant difference between the two displacement fields is the asymmetry which results in a smaller maximum displacement (+27.3 m) on the top half of the profile as compared with the bottom (-30.0 m). Unfortunately this is opposite to the trend in the measurements where a displacement of 30 +/- 18 m at 75 m depth and -26 +/- 16 m at 240 m depth were reported. Thus the improved fit to the density profile does not seem to improve the comparison with the field measurements.
The asymmetry also shows up in the perturbation density profile as shown below.

The simulation was run for a a period of time corresponding to 2.5 hours of physical time. During this time, the soliton propagates a distance of 6,335 m, giving a phase speed of 0.704 m/s. The surface current profile is shown below. The soliton is propagating to the right (positive x direction) and the surface current is to the left (negative x direction)

The shape of the current profile is almost unchanged by the details of the density fit. The maximum amplitude does change, mainly in response to the top-to-bottom asymmetries that result in lower displacements on the upper half of the profile. It is likely that if the simulation were redone targeting a 30 m displacement on the upper half of the profile, the surface currents between the two cases would be nearly identical.
4.2 Adjustment of the lower boundary position
In all previous simulations the position of the lower boundary was placed at a depth of 350 m, which coincided with the extent of the density measurements. The boundary conditions are such that the displacement is zero at the lower boundary, and thus its position may have some bearing on the computed results. In reality one may imagine that the displacement field extends beyond 350 m and thus the position of the lower boundary was adjusted in this study. The smoothed spline fit to the density data was used and the profile was simply extrapolated to depths greater than 350 m.Simulations were run with lower boundaries placed at depths of 400 and 450 m. As shown below, the main effect of moving the lower boundary downward is to displace the position of maximum negative displacement to greater depth, while leaving the position of the position maximum relatively unchanged. This actually worsens the agreement with the measurements. Since moving the lower boundary downward had the wrong effect, a case was also run by moving it upward to a depth of 300 m. The results from simulations with the lower boundary placed at 300, 350 and 400 m are shown below.

The trend is very clear; the positions of both the positive and negative displacement maxima follow the position of the lower boundary, but the effect is much greater for the negative maximum. The net result is that the position of positive maximum is very little changed, while the position of the negative maximum is only in good agreement with the measurements if a lower boundary position of 350 m is used. The asymmetry between the positive and negative maxima is also fairly insensitive to the boundary position and, as a result, this discrepancy with the measurements is not improved by moving the lower boundary either.
Comparison of the density profiles is shown below.

4.3 Minimally Smoothed Spline Fit to the Density Data
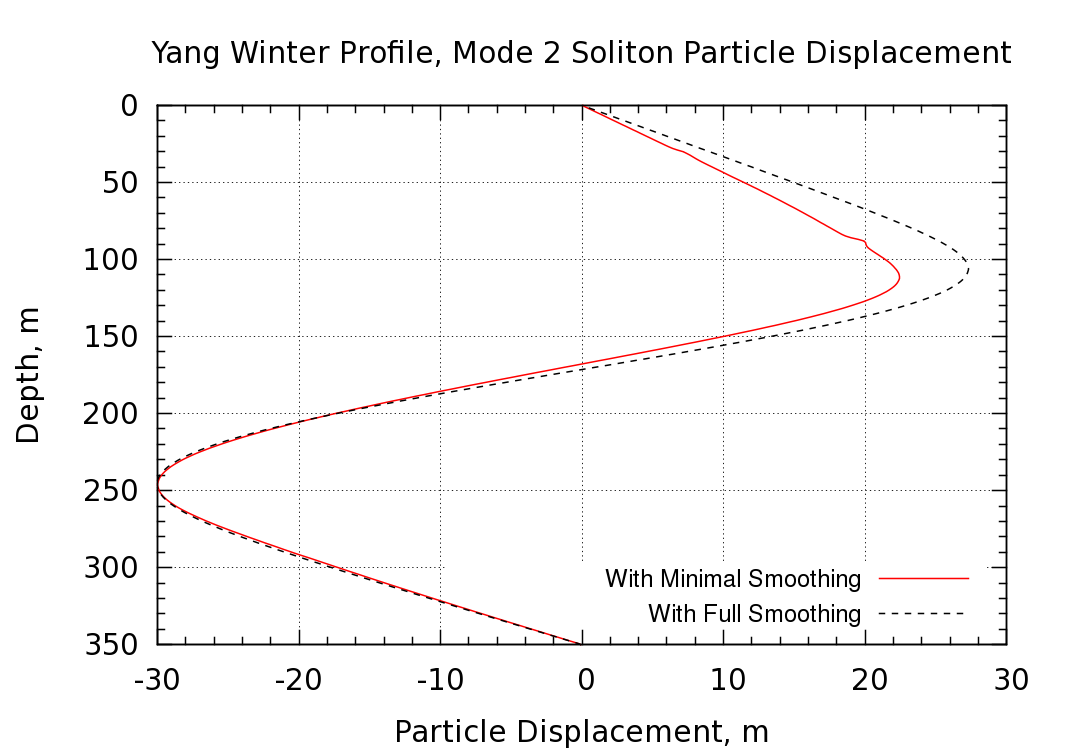
This study investigates the impact of smoothing the measured density data prior to applying the cubic spline curve fit. In all prior studies sufficient smoothing was applied to give a aesthetically pleasing fit to the data. This degree of smoothing causes some loss in the exact details of the profile, which may be important. Here much less smoothing is used in order to more faithfully represent the measured density while eliminating non-physical oscillations. At the outset of this study an attempt was made to fit the data without any smoothing whatsoever. While this can be accomplished, the resulting fit contains non-physical oscillations that put light fluid on top of heavier. Thus the smoothing parameters were increased just to the point where convective instability would take place. The resultant fit is shown below.
The resulting displacement profile is compared with the result of the fully-smoothed density profile in the following plot.

The reduced smoothing is seen to move the displacement field in the wrong direction by increasing the depth for the maximum positive displacement and reducing its value.
4.4 Other Changes to the Density Fit
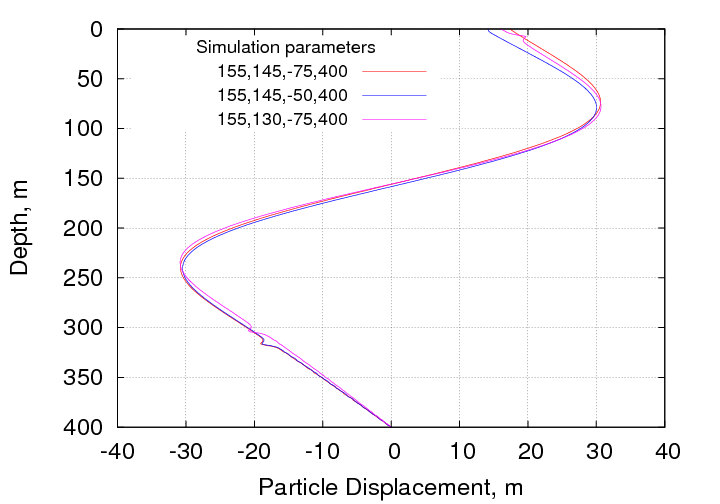
Since none of the above studies appears to improve the agreement with Yang's measurements, and attempt was made to work more in an inverse mode by starting with the results and working backward to determine the required density profile. Although this approach was not entire successful, improved agreement was achieved. A summary is shown in the plot below.
All three cases shown above produce displacement maxima close to the 75 and 240 m depths quoted by Yang. The asymmetries between the positive and negative maxima could not be reproduced, however. One common feature in the cases shown above is that all of them require a non-zero displacement on the ocean surface. Since these displacement are in the 15-18 m range there is little chance that any of these cases are realizable.
4.5 Conclusions and Speculations
It does not appear that the simulations can exactly reproduce Yang's reported values of maximum displacements for any reasonable collection of parameters. It looks like the the best match is given by the simple symmetric trigonometric fit to the density data that was used at the outset. One important aspect to note is that Yang did not measure displacements directly - he inferred these from the temperature time series taken at discrete depths. Although he reports displacement maxima at 75 and 240 m depths, these are the approximate locations of two out of twelve of his temperate sensors. In addition, Yang used KDV theory in conjunction with an unspecified fit to the density data in order to estimate displacements. It is certainly possible that these steps introduce biases into the displacement estimates. I am especially wary of the use of KDV theory for this problem since I found it to be in significant disagreement with solutions to the Euler equations, most likely due to the rather large displacements involved. Unfortunately Yang does not show detailed temperature measurements. Although there are a couple of contour plots, the temperature scale is not shown. It would be much better to compare the temperature data directly, since this would eliminate the uncertainties in estimating the displacements. The bottom line is that I think we should use the current data that go along with the simple symmetric fit shown in Study 3.Study 5: 40 m Mode 2 Soliton From Yang's Winter Density Profile
Yang observed maximum displacement amplitudes of 30 +/- 18 for the mode 2 solitons in winter. All simulations discussed above target the mean value of 30 m displacement amplitude. Here we investigate the effect of increased amplitude, within the observed range.Initially simulations were run at 48 m amplitude, which is at the upper end of the observed range. These simulations lead to instabilities that appear to be of the wave breaking type. After some trial and error it was determined that instabilities would occur for amplitudes greater than about 40 m. Thus we chose 40 m as our target amplitude, as this is slightly below the instability threshold.
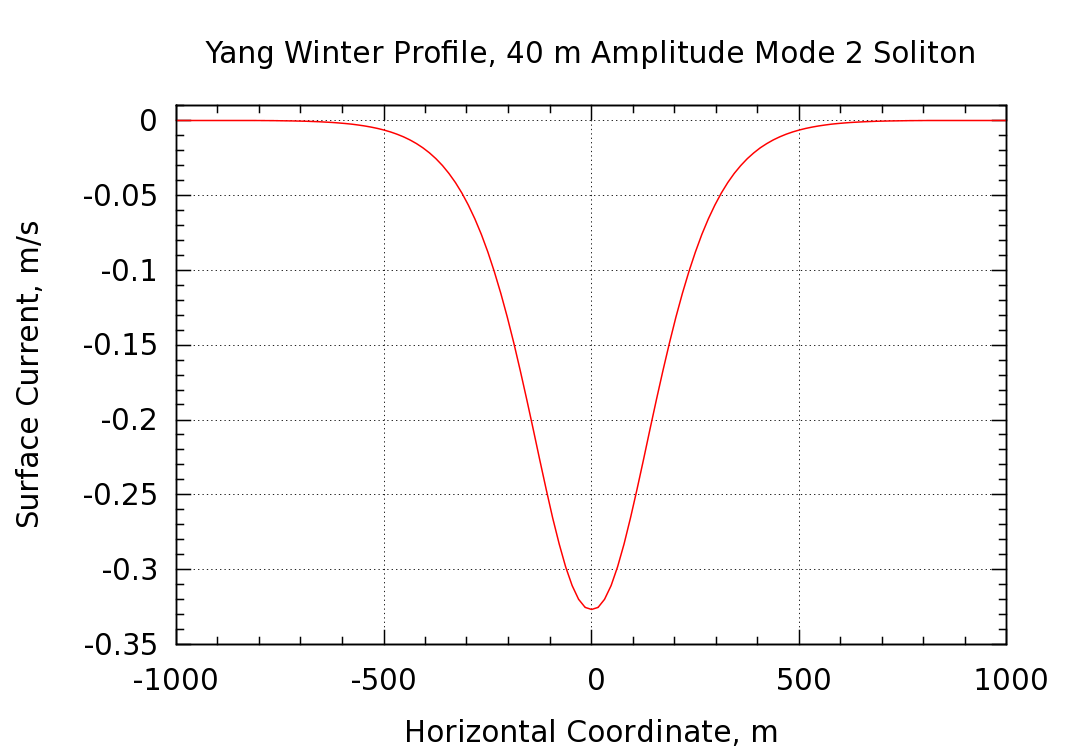
The density profile was fit with the simple symmetric trigonometric function as discussed in Study 3 above. The purification procedure discussed in Study 1 was used to produce an initial condition that is a good solution to the Euler equations. Starting from the improved initial condition, the simulation was run for a period of time corresponding to 2.5 hours of physical time. During this time, the soliton propagates a distance of 6,674 m, giving a phase speed of 0.742 m/s. The surface current profile is shown below. The soliton is propagating to the right (positive x direction) and the surface current is to the left (negative x direction)

An animation of the surface current evolution can be viewed by clicking the image below

The soliton propagates at nearly constant speed and amplitude and the surface current follows suit. A very slight undular tail develops and propagates to the left behind the main surface current pulse.
The particle vertical displacement and density perturbation profiles at the center of the soliton (where the displacements are maximized) are shown in the following two plots.


Study 6: Mode 1 Soliton From Yang's Winter Density Profile
Although Yang observed mainly mode 2 solitons during the winter, it is of interest to also compute a mode 1 soliton for comparison. Here we consider a mode 1 wave with a maximum displacement amplitude of 30 m.The density profile was fit with the simple symmetric trigonometric function as discussed in Study 3 above. The purification procedure discussed in Study 1 was used to produce an initial condition that is a good solution to the Euler equations. Starting from the improved initial condition, the simulation was run for a period of time corresponding to 2.5 hours of physical time. During this time, the soliton propagates a distance of 13,589 m, giving a phase speed of 1.510 m/s. The surface current profile is shown below. The soliton is propagating to the right (positive x direction) and the surface current is also to the right (positive x direction)

An animation of the surface current evolution can be viewed by clicking the image below

The surface current for the mode 1 wave is seen to develop a pronounced undular tail as time goes on. The tail is significantly large that it extracts energy from the main pulse, and thus the maximum suface current decreases in time. Since this behavior is rather different from the mode 2 wave (where almost no tail develops), several checks were performed to ensure that the mode 1 simulation is sound. The KDV solver which provides the initial condition is unified so that the only difference between computing a mode 1 and a mode 2 soliton is in solving the eigenvalue problem for the mode shape. Only mild transients appeare when the model 1 KDV solution is advanced in time in the Euler equation solver, indicating that the initial condition is sound. It was found that the extent to which an undular tail develops is dependent on the soliton amplitude. Mode 1 waves with amplitudes on the order of a few meters do not produce tails. Tails were observed for amplitudes greater than about 5 m, and become more pronounced as the amplitude is increased. Several references to undular tails were found via a google search and a few images of similar looking wave forms were spotted. Thus at this point it appears that the undular tail is a realistic characteristic of a large amplitude mode 1 wave.
The particle vertical displacement and density perturbation profiles at the center of the soliton (where the displacements are maximized) are shown in the following two plots.


grid file for contour plots
vorticity data file for contour plots
density data file for contour plots
vorticity data file for contour plots
density data file for contour plots
Study 7: Mode 2 Soliton From the Case 1 Density Profile
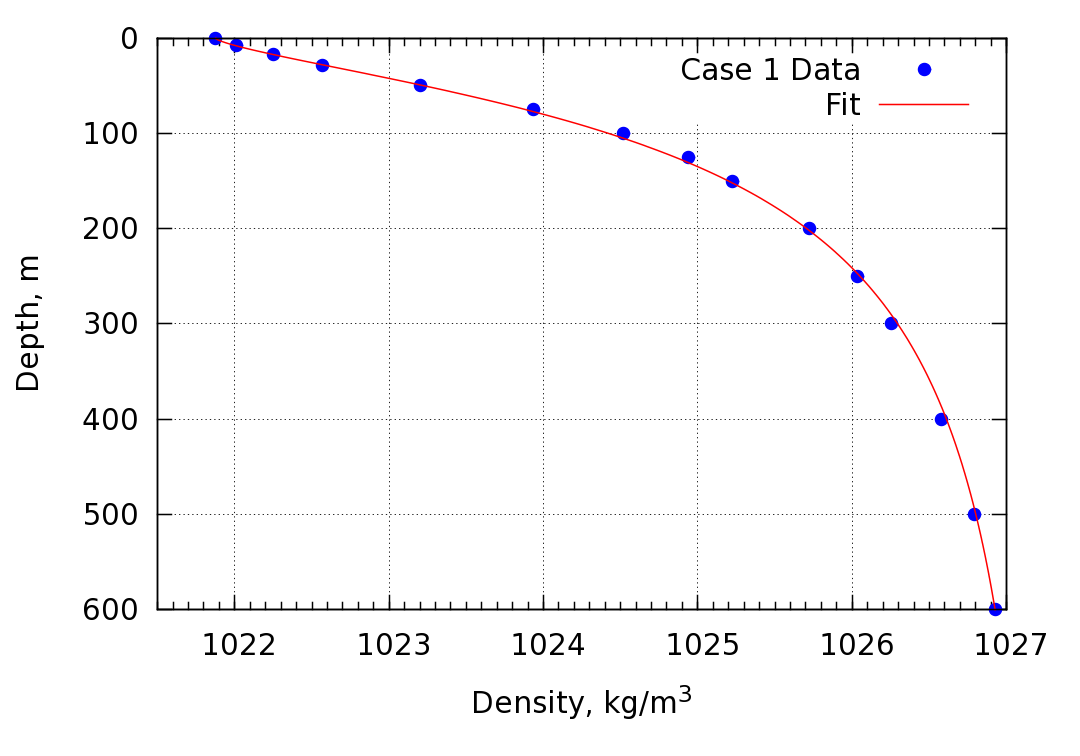
This study involves the simulation of a mode 2 soliton with an amplitude of ~30 m propagating in the duct corresponding to the case 1 density profile from the figures in the word document. The data was curve-fit in order to provide a continuous density distribution to be used in the simulation. The fit is shown below
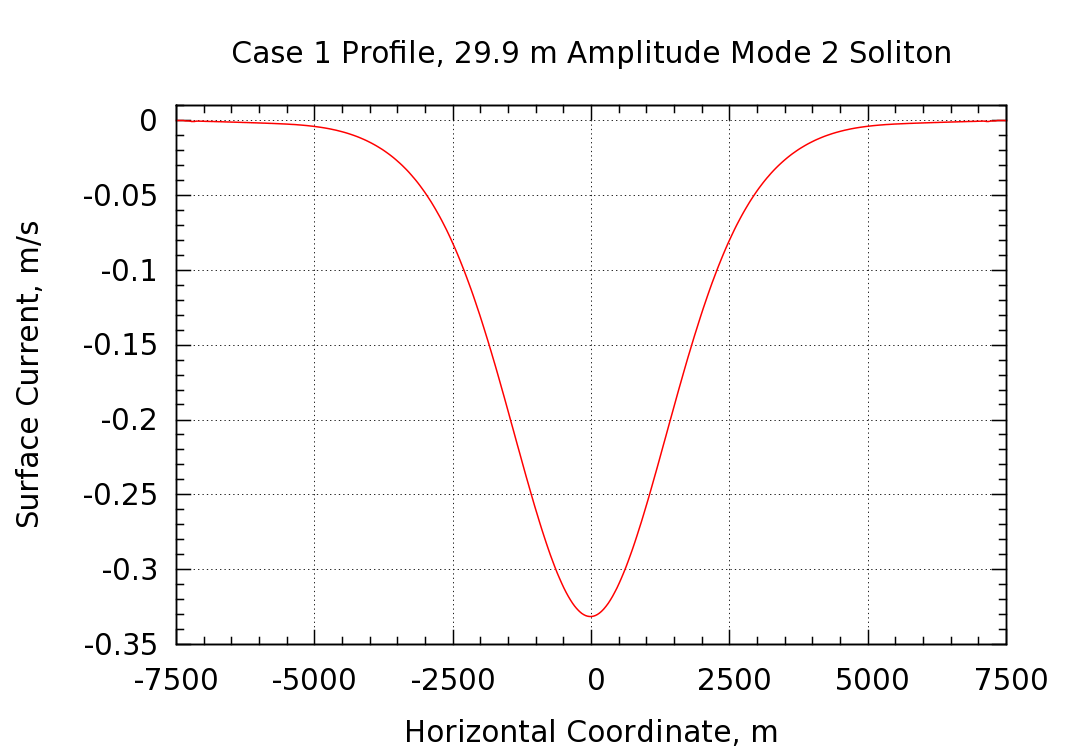
The simulation was first initialized with the shallow water water KDV solution. Since this solution is only approximate, the purification procedure described in the Study 1 discussion above was used to arrive at an initial condition that is a much better solution to the Euler equations. The displacement amplitude changes slightly during the purification procedure, making it necessary to iterate in order to arrive at the improved initial condition with the desired amplitude. Two iteration cycles were undertaken and thus the target amplitude was not hit exactly. The simulation described below has a displacement amplitude of 29.9 m whereas 30 m was desired. Starting from the improved initial condition, the simulation was run for a period of time corresponding to 4.17 hours of physical time. During this time, the soliton propagates a distance of 11,378 m, giving a phase speed of 0.759 m/s. The surface current profile is shown below. The soliton is propagating to the right (positive x direction) and the surface current is to the left (negative x direction)

Surface current data file
An animation of the surface current evolution can be viewed by clicking the image below
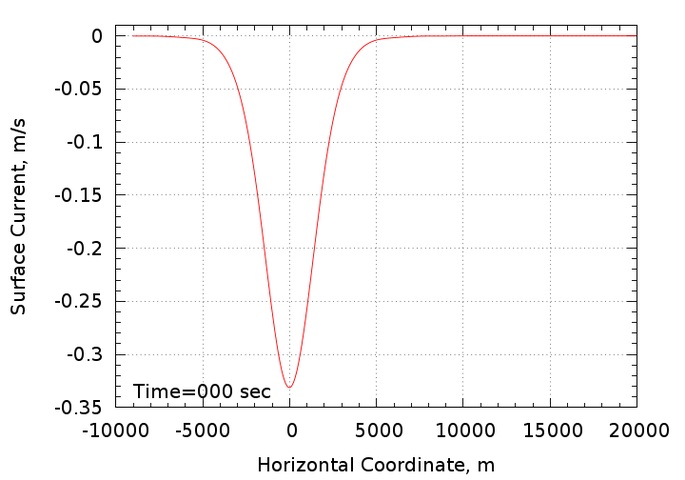
The soliton propagates at nearly constant speed and amplitude and the surface current follows suit. A very slight dispersive leading edge develops and propagates out in front of the main surface current pulse.
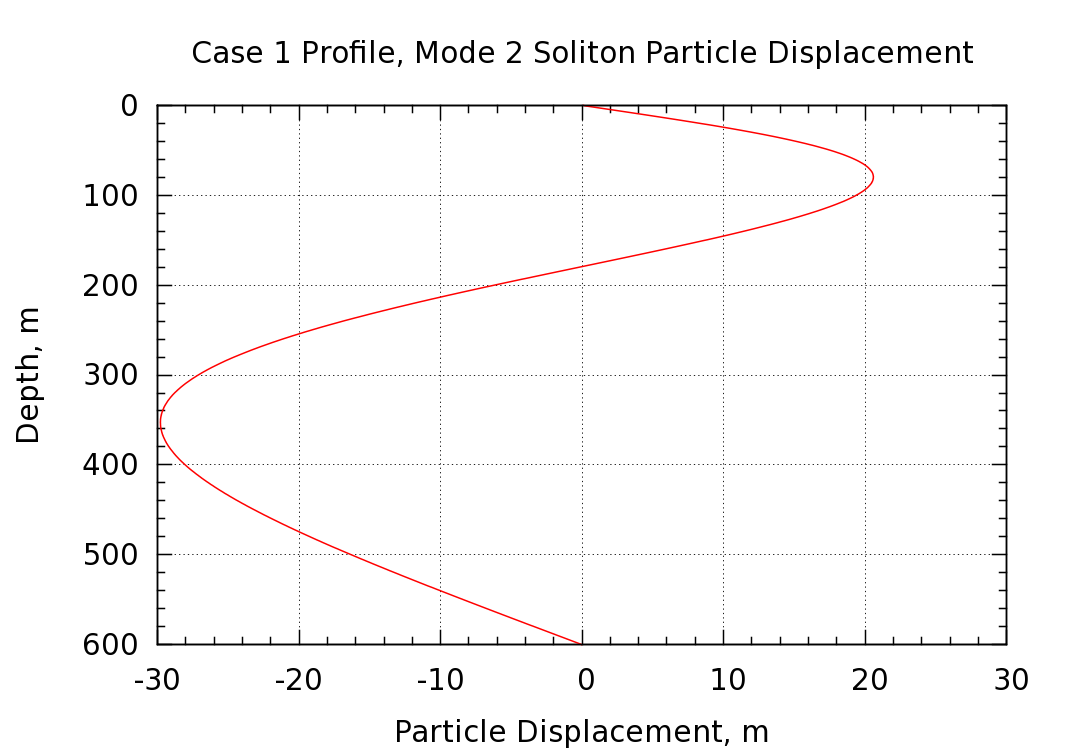
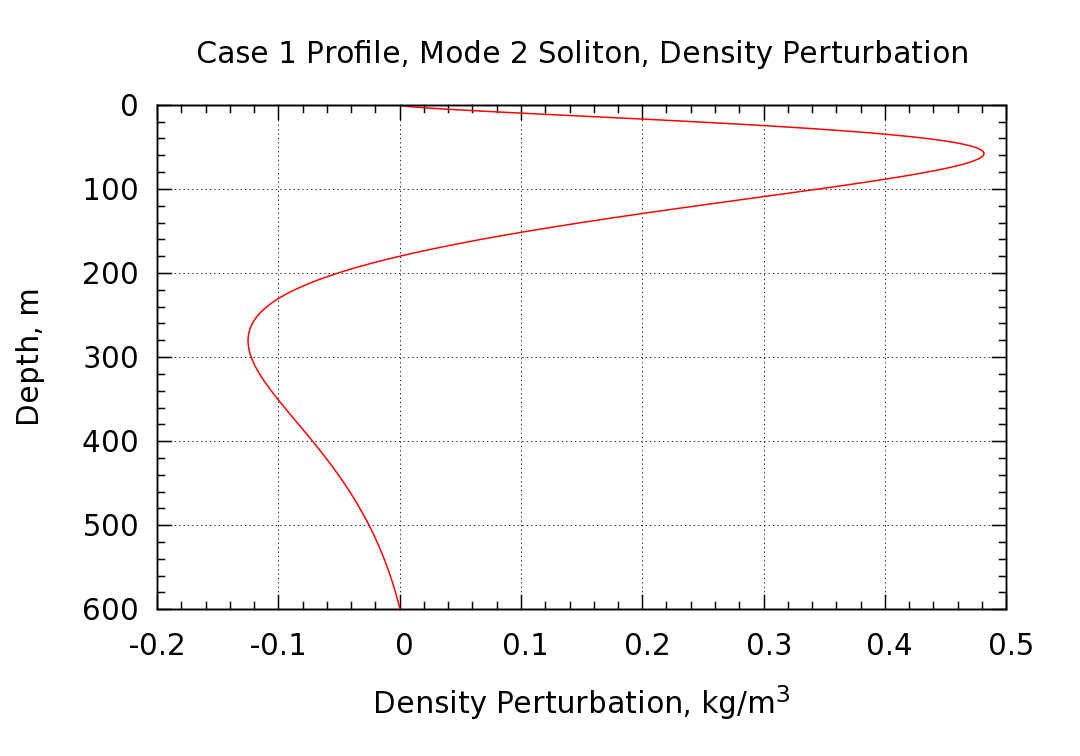
The particle vertical displacement and density perturbation profiles at the center of the soliton (where the displacements are maximized) are shown in the following two plots.
Comparing with the Study 3 results, we see that the phase speed, the maximum surface current, and the shape of the surface current pulse are all fairly similar. The main difference is in the width of the surface current pulse. The pulse in Study 3 has a half maximum half width of approximately 190 m, whereas Study 4 has a half width of about 1680 m. This is larger by a factor of 8.8. This substantial difference is related to differences in the shapes of the stability ducts for the two cases. The plot below shows a comparison of the buoyancy frequencies for the two cases.
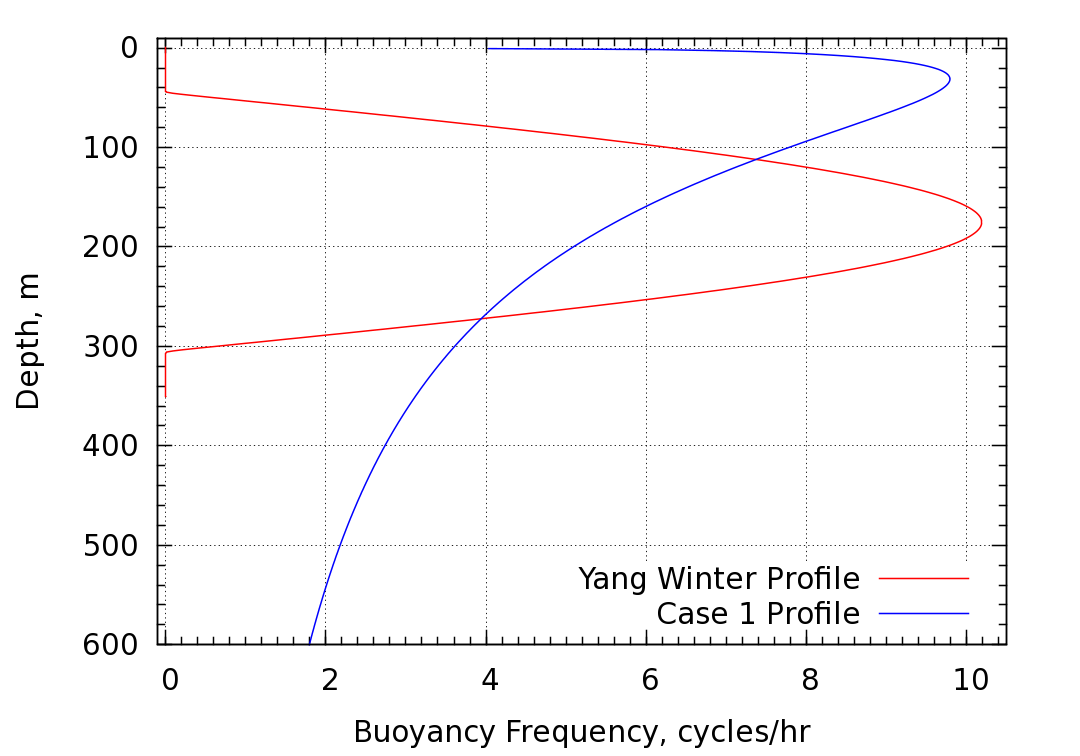
Indeed there are marked differences between the two ducts. The Yang winter density data is fit well with a function that produces a symmetric duct sandwiched between regions of neutral stability. The Case 1 duct, on the other hand, is quit asymmetric and contains no region of neutral stability on either side. The gradual reduction in buoyancy frequency with depth for Case 1 results in an effective duct with that is much greater than for Yang's data.
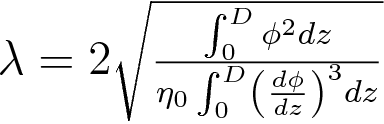
According to KDV theory the soliton horizontal wavelength is given by
where 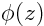 is the modal function for vertical displacement,
is the modal function for vertical displacement,
 is the maximum displacement, and
is the maximum displacement, and  is
the depth of water containing the soliton. The modal function satisfies
the equation
is
the depth of water containing the soliton. The modal function satisfies
the equation
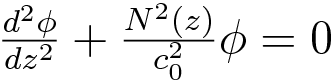
and thus depends only on the buoyancy frequency,  , and
the boundary conditions. The soliton phase speed,
, and
the boundary conditions. The soliton phase speed, 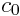 ,
appears as an eigenvalue. The above two equations demonstrate that the
soliton horizontal wavelength depends on the maximum displacement amplitude
as well as the indicated moments of the modal function, with the latter
depending on the buoyancy frequency profile. Since the Yang winter profile
soliton and the Case 1 soliton have the same target maximum displacement
amplitude (30 m), differences in the horizontal wavelength must arise from
differences in the moments of the modal functions. In order to investigate
this line of reasoning further, the modal functions and their derivatives
are plotted below.
,
appears as an eigenvalue. The above two equations demonstrate that the
soliton horizontal wavelength depends on the maximum displacement amplitude
as well as the indicated moments of the modal function, with the latter
depending on the buoyancy frequency profile. Since the Yang winter profile
soliton and the Case 1 soliton have the same target maximum displacement
amplitude (30 m), differences in the horizontal wavelength must arise from
differences in the moments of the modal functions. In order to investigate
this line of reasoning further, the modal functions and their derivatives
are plotted below.
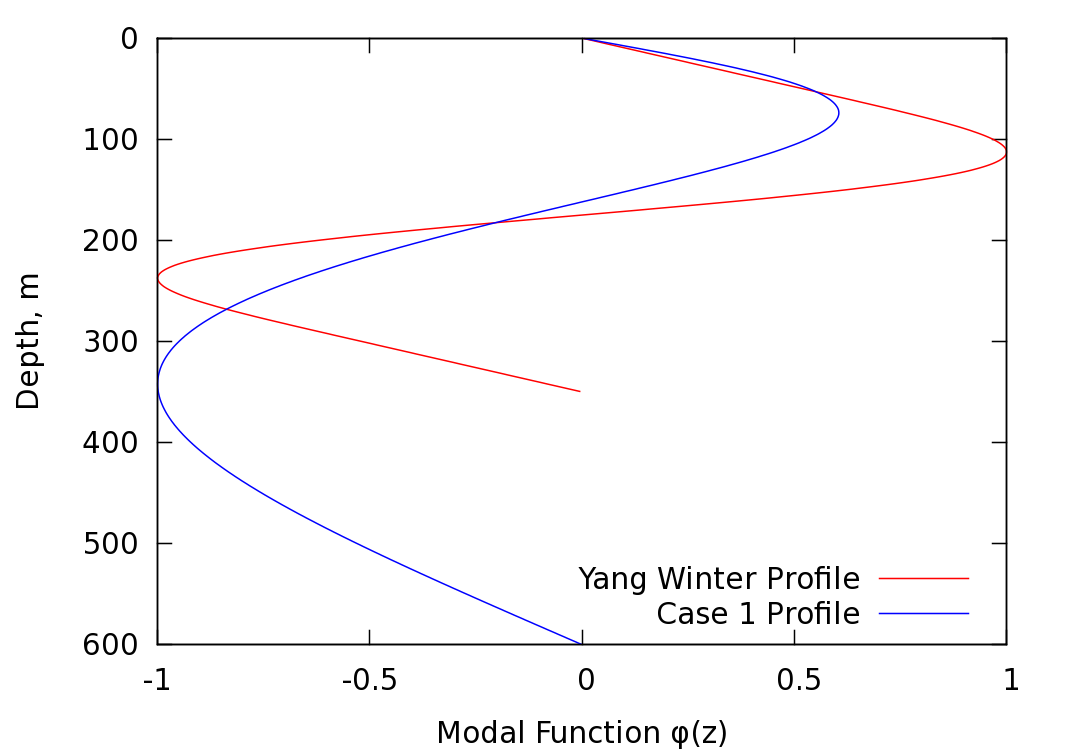
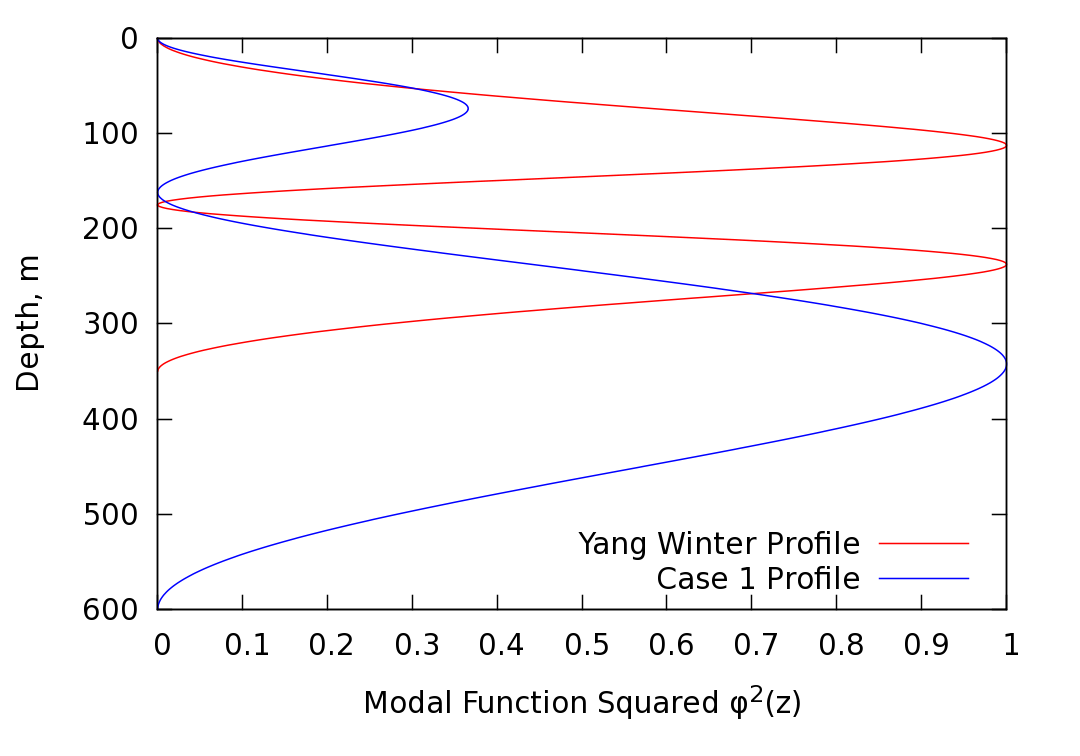
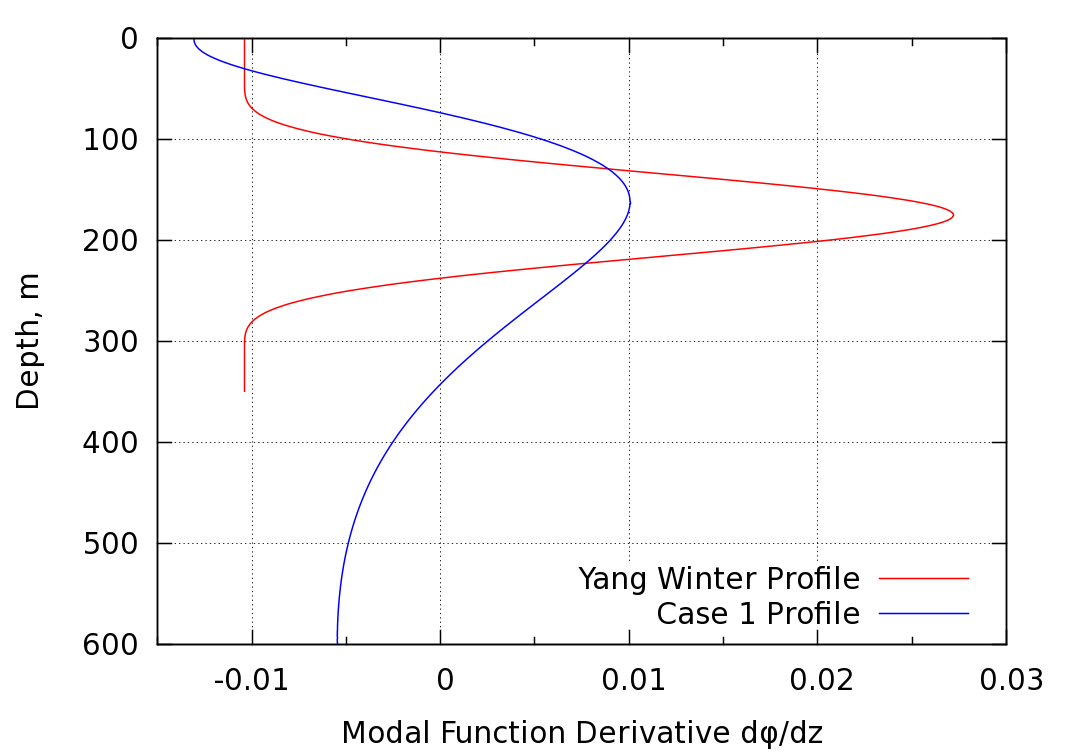
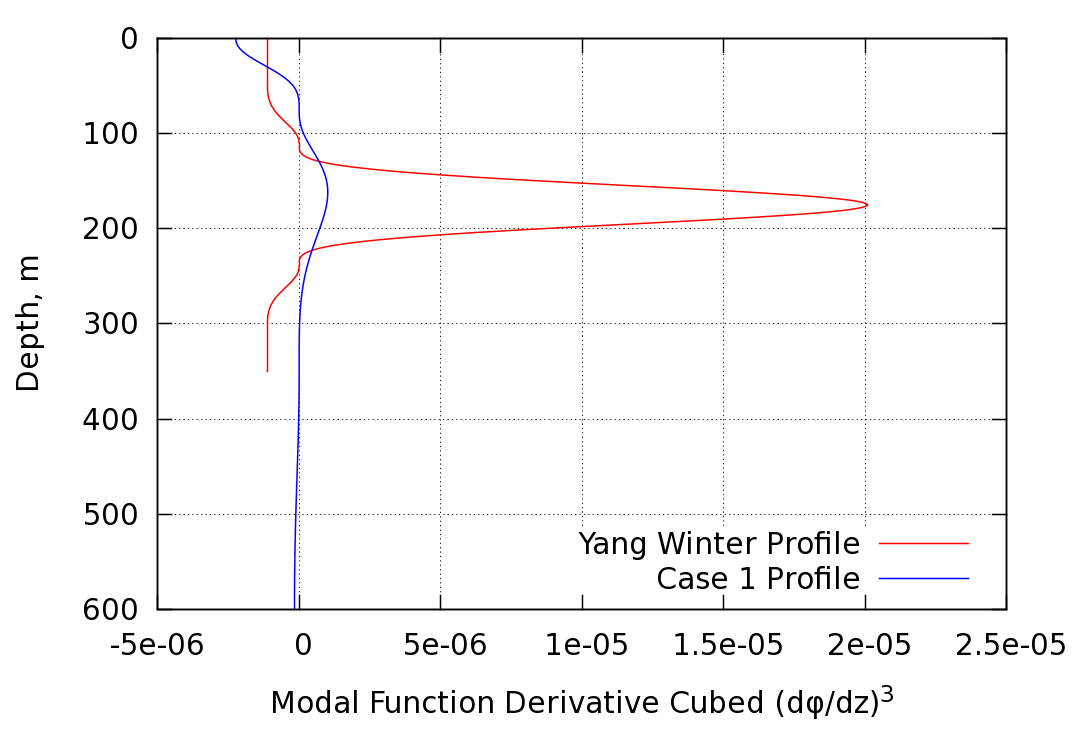
These plots demonstrate that the most significant difference between the two soliton cases is in the profile, which appears in the
denominator of the expression for the horizontal wavelength. The Yang winter
profile soliton has much larger
profile, which appears in the
denominator of the expression for the horizontal wavelength. The Yang winter
profile soliton has much larger  values, which result
in a significantly smaller horizontal wavelength as compared to the Case 1
soliton. In simpler terms, the relatively narrow Yang winter stability duct
results in a more compact modal function, thus producing a larger first
derivative, which leads to a smaller horizontal wavelength.
values, which result
in a significantly smaller horizontal wavelength as compared to the Case 1
soliton. In simpler terms, the relatively narrow Yang winter stability duct
results in a more compact modal function, thus producing a larger first
derivative, which leads to a smaller horizontal wavelength.
The above analysis demonstrates that the horizontal wavelength is a fairly non-linear function of the stability duct width.
An animation of the surface current evolution can be viewed by clicking the image below

The soliton propagates at nearly constant speed and amplitude and the surface current follows suit. A very slight dispersive leading edge develops and propagates out in front of the main surface current pulse.
The particle vertical displacement and density perturbation profiles at the center of the soliton (where the displacements are maximized) are shown in the following two plots.


Comparing with the Study 3 results, we see that the phase speed, the maximum surface current, and the shape of the surface current pulse are all fairly similar. The main difference is in the width of the surface current pulse. The pulse in Study 3 has a half maximum half width of approximately 190 m, whereas Study 4 has a half width of about 1680 m. This is larger by a factor of 8.8. This substantial difference is related to differences in the shapes of the stability ducts for the two cases. The plot below shows a comparison of the buoyancy frequencies for the two cases.

Indeed there are marked differences between the two ducts. The Yang winter density data is fit well with a function that produces a symmetric duct sandwiched between regions of neutral stability. The Case 1 duct, on the other hand, is quit asymmetric and contains no region of neutral stability on either side. The gradual reduction in buoyancy frequency with depth for Case 1 results in an effective duct with that is much greater than for Yang's data.
According to KDV theory the soliton horizontal wavelength is given by

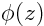 is the modal function for vertical displacement,
is the modal function for vertical displacement,
 is the maximum displacement, and
is the maximum displacement, and  is
the depth of water containing the soliton. The modal function satisfies
the equation
is
the depth of water containing the soliton. The modal function satisfies
the equation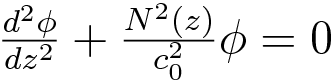
 , and
the boundary conditions. The soliton phase speed,
, and
the boundary conditions. The soliton phase speed, 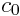 ,
appears as an eigenvalue. The above two equations demonstrate that the
soliton horizontal wavelength depends on the maximum displacement amplitude
as well as the indicated moments of the modal function, with the latter
depending on the buoyancy frequency profile. Since the Yang winter profile
soliton and the Case 1 soliton have the same target maximum displacement
amplitude (30 m), differences in the horizontal wavelength must arise from
differences in the moments of the modal functions. In order to investigate
this line of reasoning further, the modal functions and their derivatives
are plotted below.
,
appears as an eigenvalue. The above two equations demonstrate that the
soliton horizontal wavelength depends on the maximum displacement amplitude
as well as the indicated moments of the modal function, with the latter
depending on the buoyancy frequency profile. Since the Yang winter profile
soliton and the Case 1 soliton have the same target maximum displacement
amplitude (30 m), differences in the horizontal wavelength must arise from
differences in the moments of the modal functions. In order to investigate
this line of reasoning further, the modal functions and their derivatives
are plotted below.



These plots demonstrate that the most significant difference between the two soliton cases is in the
 profile, which appears in the
denominator of the expression for the horizontal wavelength. The Yang winter
profile soliton has much larger
profile, which appears in the
denominator of the expression for the horizontal wavelength. The Yang winter
profile soliton has much larger  values, which result
in a significantly smaller horizontal wavelength as compared to the Case 1
soliton. In simpler terms, the relatively narrow Yang winter stability duct
results in a more compact modal function, thus producing a larger first
derivative, which leads to a smaller horizontal wavelength.
values, which result
in a significantly smaller horizontal wavelength as compared to the Case 1
soliton. In simpler terms, the relatively narrow Yang winter stability duct
results in a more compact modal function, thus producing a larger first
derivative, which leads to a smaller horizontal wavelength.The above analysis demonstrates that the horizontal wavelength is a fairly non-linear function of the stability duct width.
References
Benjamin 1967, "Internal waves of permanent form
in fluids of great depth"
Davis and Acrivos 1967, "Solitary internal waves in
deep water"
Laughman, Fritts, and Werne 2011, "Comparisons of
predicted bore evolutions by the Benjamin-Davis-Ono and Navier-Stokes
equations for idealized mesopause thermal ducts"
Olsthoorn, Baglaenko, and Stastna 2013, "Analysis
of asymmetries in propagating mode-2 waves"
Grisouard, Staquet, and Gerkema 2011,
"Generation of internal solitary waves in a pycnocline by an internal wave
beam: a numerical study"